Impact of Vaccination and Testing Levels on the Dynamics of the COVID-19 Pandemic and its Cessation

A simple statistical analysis of the accumulated and daily numbers of new COVID-19 cases and deaths per capita was performed with the use of recent datasets for European and some other countries and regions in order to find correlations with the testing and vaccination levels. It was shown that vaccination can significantly reduce the likelihood of deaths. However, existing vaccines do not prevent new infections. It looks that vaccinated individuals can spread the infection as intensely as unvaccinated ones and it is too early to lift quarantine restrictions in Europe and most other countries. The constant appearance of new cases due to re-infection increases the likelihood of new coronavirus strains, including very dangerous. As existing vaccines are not able to prevent this, it remains to increase the number of tests per registered case. If the critical value of the tests per case ratio (around 520) is exceeded, one can hope to stop the occurrence of new cases.

To investigate the effectiveness of quarantine, testing and vaccination, different relative characteristics (calculated per capita) can be used. In particular, such values are regularly reported by COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU) [1]. The accumulated numbers of COVID-19 Cases per Capita (CC) was used in [2] to investigate the influence of demographic factors in European countries. In the end of June 2021 the CC values varied more than 9 times for different European countries but showed no visible dependencies on the volume of population, its density, and the level of urbanization. In this paper we will try to find some statistical correlation between CC values and the accumulated number of Tests per Capita (TC) and the tests per cases ratio TC/CC. We will try also to find similar relationships for the accumulated numbers of Deaths per Capita caused by coronavirus (DC) and the mortality rate DC/CC versus TC and TC/CC.

The current dynamics of the pandemic is characterized by daily increases in the number of cases. The daily numbers of new COVID-19 cases per capita (DCC) was used in [3] to find some seasonal trends of the COVID-19 pandemic in the EU and some other countries. This characteristic and the daily numbers of new deaths per capita caused by coronavirus (DDC) are very important in order to investigate the efficiency of vaccinations. In particular, it was shown in [4] that rather high numbers of fully vaccinated people per capita (VC) did not protect the population of Israel against a new pandemic wave in the summer of 2021. In this paper we will try to find a correlation between DCC, DDC and VC values.

We will use the data sets regarding the relative characteristics (per capita) reported by JHU as of September 1, 2021 [1]. The figures corresponding to the version of the JHU data available on September 12, 2021 are presented in table 1. We cannot fix the date September 12 for all the data, since many figures appear in the JHU tables with the delay. The accumulated characteristics: CC (number of cases per million), DC (number of deaths per million), TC (number of tests per thousand), VC (percentage of fully vaccinated people) are taken without smoothing.

Since daily characteristics DCC (new cases per million) and DDC (new deaths per million) are very random and demonstrate some weekly periodicity, we will use smoothed (averaged) values calculated and displayed by JHU with the use of figures registered during the previous 7 days. This smoothing procedure differs from one proposed in [5-7], where the values registered in the nearest 7 days were used.

We will use the linear regression to calculate the regression coefficients r and the coefficients a and b of corresponding best fitting straight lines, [8]:

$y=a+bx\text{ (1)}$

where x are TC, TC/CC, and VC values and y are CC, DC, DC/CC, DCC, DDC, and DDC/DCC values.

We will use also the F-test for the null hypothesis that says that the proposed linear relationship (1) fits the data sets. The experimental values of the Fisher function can be calculated with the use of the formula:

$F=\frac{r^2(n-m)}{(1-r^2)(m-1)}\text{ (2)}$

where n is the number of observations (number of countries and regions taken for statistical analysis); m = 2 is the number of parameters in the regression equation [8]. The corresponding experimental values F have to be compared with the critical values $F_C(k_1,k_2)$ of the Fisher function at a desired significance or confidence level ( $k_1=m-1$ , $k_2=n-m,$ see, e.g., [9]). If $F/F_C(k_1,k_2)<1$ , the null hypothesis is not supported by the results of observations. The highest values of correspond to the most reliable hypotheses (see, e.g., [10]).

Table 1: Accumulated and daily characteristics of the COVID-19 pandemic dynamics in European and some other countries and regions as of September 1, 2021 (figures corresponding to other days in May-September 2021 are specified in notes) [1].
Country	Total cases per million CC	Total death per million DC	Total tests per thousand TC	People fully vaccinated, %, VC	New cases per million, smoothed DCC	New deaths per million, smooth. DDC
European countries
Monaco	81250	835.02	no data	57.071	173.511	0
Holy See (Vatican City)	33251.232	no data	no data	no data	0	0
Malta	70442.161	857.036	2321.107	80.27	94.116	1.111
San Marino	156748.02	2646.281	no data	70.49	163.817	0
Netherlands	115262.92	1069.871	736.142	62.642	152.897	0.516
Belgium	102086.65	2182.021	1614.388	70.14	176.822	0.418
United Kingdom	100531.05	1950.911	3590.956	63.08	492.479	1.556
Liechtenstein	85690.385	1542.322	1624.614	53.55	115.768	0
Luxembourg	119568.88	1307.47	5400.155	56.18	133.222	0
Germany	47435.24	1099.66	838.0142	60.34	116.255	0.293
Italy	75313.524	2141.716	1397.101	61.1	104.34	0.89
Switzerland	89824.971	1251.449	1079.174	51.23	289.779	0.82
Andorra	194508.36	1680.585	2709.9182	54.08	59.098	0
Denmark	59838.969	444.842	6874.115	72.59	147.027	0.319
Czech Republic	156601.03	2834.99	no data	53.6	18.556	0.226
Poland	76435.59	1993.756	513.568	49.8	6.675	0.11
Portugal	102232.48	1746.374	1682.166	75.37	191.4	1.166
Slovakia	72357.046	2297.863	7527.671	39.81	21.897	0.026
Albania	51295.644	870.539	256.5373	22.58	298.55	0.895
Austria	76318.424	1191.52	8492.748	57.82	157.563	0.079
France	101653.62	1702.542	no data	60.19	233.095	1.672
Hungary	84338.524	3120.043	636.628	57.2	17.705	0.059
Turkey	75400.291	670.251	901.9	43.94	232.817	3.004
Slovenia	128907.03	2140.737	699.719	43.58	227.681	0.481
Moldova	66626.077	1591.938	393.6221	17.29	81.226	0.923
Spain	104008.15	1807.073	1186.8214	72	142.652	2.39
Serbia	112611.98	1073.833	741.032	41.31	369.204	1.554
Romania	57518.879	1808.418	477.1551	26.89	54.05	1.031
North Macedonia	85179.009	2863.644	553.0025	25.88	399.42	14.336
Greece	56971.017	1318.034	1506.965	55.43	285.9	2.893
Bosnia and Herzegovina	65807.17	3007.545	350.723	13.069	161.967	2.495
Croatia	91826.187	2042.798	623.2756	39.68	133.629	0.98
Ireland	71090.272	1025.908	1348.36	68.09	341.367	0.573
	CC	DC	TC	VC	DCC	DDC
Ukraine	54916.644	1312.863	276.267	8.99	49.815	1.479
Bulgaria	66334.622	2747.709	620.0831	17.12	223.483	6.981
Belarus	51174.183	401.467	827.889	14.152	157.02	1.195
Montenegro	184628.32	2757.738	no data	29.45	959.886	8.416
Lithuania	111355.9	1698.6	1723.318	56.23	220.882	3.399
Latvia	76652.951	1381.409	1788.7417	40.96	120.136	0.689
Estonia	107428.53	975.711	1335.17	41.27	261.526	0.862
Sweden	111013.72	1446.04	no data	56.212	102.487	0.253
Norway	29605.742	150.394	1318.59	58.07	253.402	0.209
Finland	23044.824	185.64	1201.377	51.1	108.809	0.309
Iceland	31616.962	96.109	1715.983	76.82	214.269	1.248
Other countries and regions
United States	118336.96	1929.465	1604.422	51.91	503.381	4.186
North America	79327.442	1643.263	no data	42.43	338.245	3.973
Argentina	113822.04	2455.936	293.9	32.42	112.357	3.255
Brazil	97218.938	2715.737	148.2138	29.68	105.93	3.007
South America	85023.252	2605.171	no data	31.06	76.457	2.336
South Africa	46420.892	1373.972	275.411	10.23	154.656	4.823
Africa	5694.404	143.37	no data	2.86	20.617	0.535
India	23580.97	315.434	375.471	10.9	30.696	0.324
Israel	123209.17	806.164	2675.281	62.52	1058.958	2.893
Japan	11991.372	128.131	166.789	46.85	161.421	0.434
South Korea	4978.074	44.888	241.129	31.74	33.647	0.128
Qatar	79477.254	205.424	856.443	73.44	65.859	0.049
Asia	15035.556	222.955	no data	28.91	54.181	0.868
Australia	2193.25	39.514	1233.936	28.37	48.306	0.166
World	27737.424	575.503	no data	27.3	81.926	1.232
Figures corresponding different days in 2021: 1 09-02; 2 08-29; 3 06-13; 4 08-26; 5 08-30; 6 08-31; 7 08-27; 8 05-24; 9 09-07.

The results of the linear regression application are presented in table 2 and figures 1-3. We have used the data sets corresponding to the European countries and complete datasets with the information about some other countries and regions. Thus, we have two different numbers of observations n for every application of the linear relationship (1). Due to the lack of some data, the numbers n are different for different relationships (e.g., versus TC and versus VC). Corresponding values of the regression coefficients r, coefficients a and b; values of the Fisher function F, $F_C(k_1,k_2)$ and $F/F_C(k_1,k_2)$ are shown in table 2. The best fitting lines (1), calculated with the use of corresponding values a and b are shown in figures 1-3 by solid lines for European datasets and by dashed lines for complete datasets. The values CC, DC, DC/CC, DCC, DDC, and DDC/DCC are represented by “crosses” for European countries and by “circles” for other countries and regions.

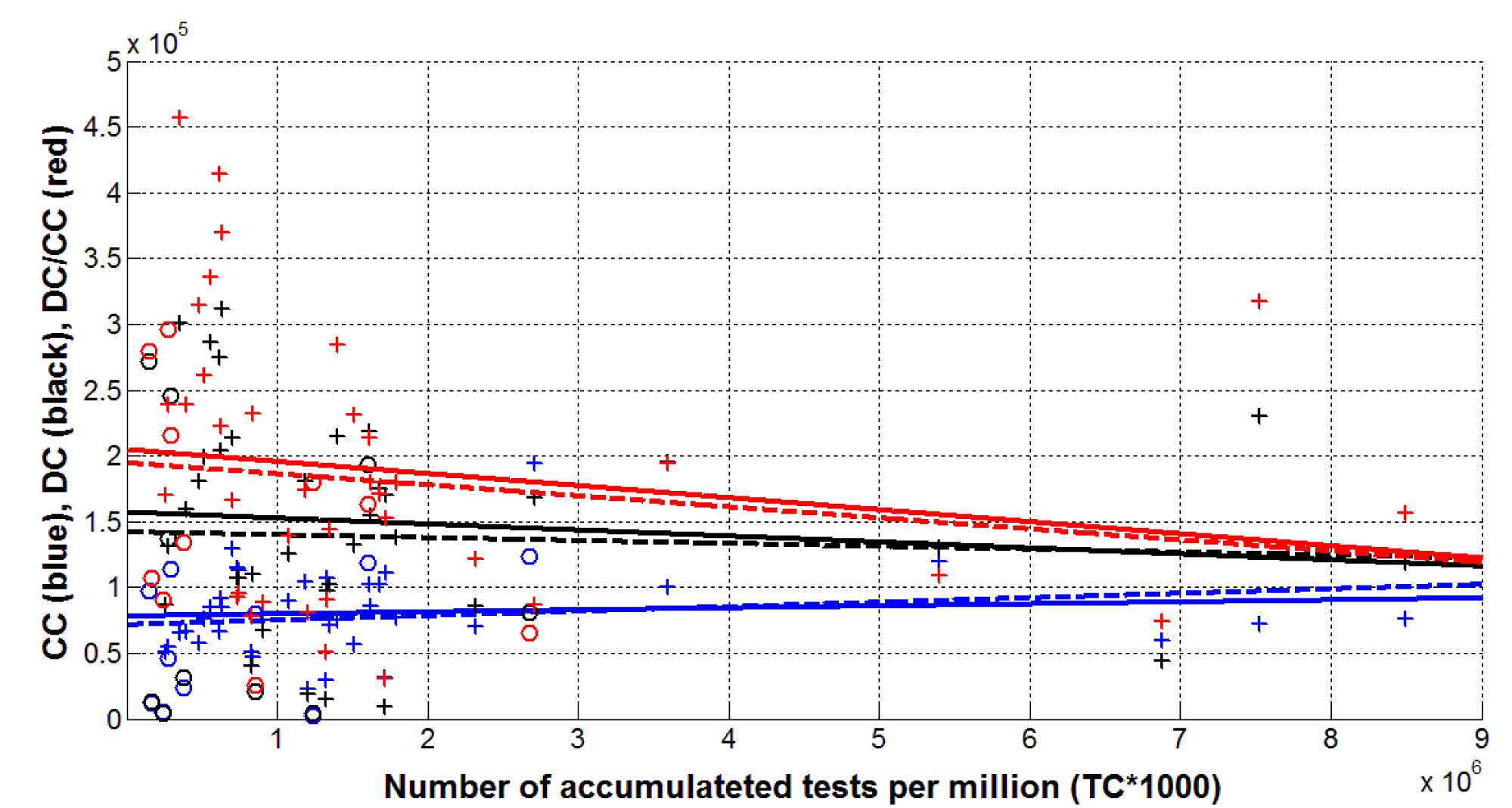
Table 2 and figure 1 illustrate that there is no visible correlation between all the relative accumulated characteristics (CC, DC and DC/CC) and the accumulated number of tests per capita (TC), since $F/F_C(k_1,k_2)<1$ for all 6 calculations (see the rows in table 2 corresponding to figure 1). Statistical analysis did not confirm the common view that more tests per capita can better identify patients and lead to an increase in CC and DC values. A very weak growth trend with increasing number of tests we see for CC values (see blue lines in figure 1). For values DC and DC/CC, black and red lines illustrate opposite trends. This probably triggers the fact that more tests can detect and isolate patients more quickly, slowing the spread of infection and the number of deaths. The competition of these two tendencies results in an almost imperceptible correlation. It looks that it is impossible to stop the pandemic by increasing the number of tests per capita.

Table 2: Optimal values of parameters in eq. (1), correlation coefficients and the results of Fisher test applications.
Number of Figure, relationship	Num-ber of ob- ser va-tions n	Correlation coefficient R	Optimal values of parameters a in eq. (1)	Optimal values of parameters b in eq. (1)	Experimental value of the Fisher function F, eq. (2), m=2	Critical value of Fisher Function Fc(1,n-2) for the confidence level 0.1, [9]	F/Fc
1, CC versus TC	37	0.0952	7.8115e+04	1.5147	0.3202	2.86	0.1120
	47	0.1728	7.1474e+04	3.3914	1.3848	2.84	0.4876
1, DC versus TC	37	-0.1176	1.5699e+03	-0.0454	0.4906	2.86	0.1715
	47	-0.0478	1.4190e+03	-0.0218	0.1031	2.84	0.0363
1, DC/CC versus TC	37	-0.1793	0.0205	-9.1515e-07	1.1620	2.86	0.4063
	47	-0.1565	0.0194	-8.3788e-07	1.1293	2.84	0.3977
2, CC versus TC/CC	37	-0.2471	8.7751e+04	-2.7460e+05	2.2752	2.86	0.7955
	47	-0.3580	8.2349e+04	-1.5841e+05	6.6143	2.84	2.3290
2, DC versus TC/CC	37	-0.3191	1.7042e+03	-8.6173e+03	3.9668	2.86	1.3870
	47	-0.3161	1.4969e+03	-3.2532e+03	4.9951	2.84	1.7588
2, DC/CC versus TC/CC	37	-0.2460	0.0210	-0.0877	2.2544	2.86	0.7883
	47	-0.0790	0.0184	-0.0095	0.2826	2.84	0.0995
3, DCC versus VC	43	-0.1004	234.6744	-0.8581	0.4171	2.85	0.1464
	58	0.1245	136.6035	1.2095	0.8821	2.8	0.3150
3, DDC versus VC	43	-0.3730	4.1071	-0.0521	6.6256	2.85	2.3248
	58	-0.2972	3.2549	-0.0359	5.4255	2.8	1.9377
3, DDC/DCC versus VC	43	-0.5087	0.0194	-2.3335e-04	14.3156	2.85	5.0230
	58	-0.5855	0.0227	-2.8822e-04	29.2106	2.8	10.4324

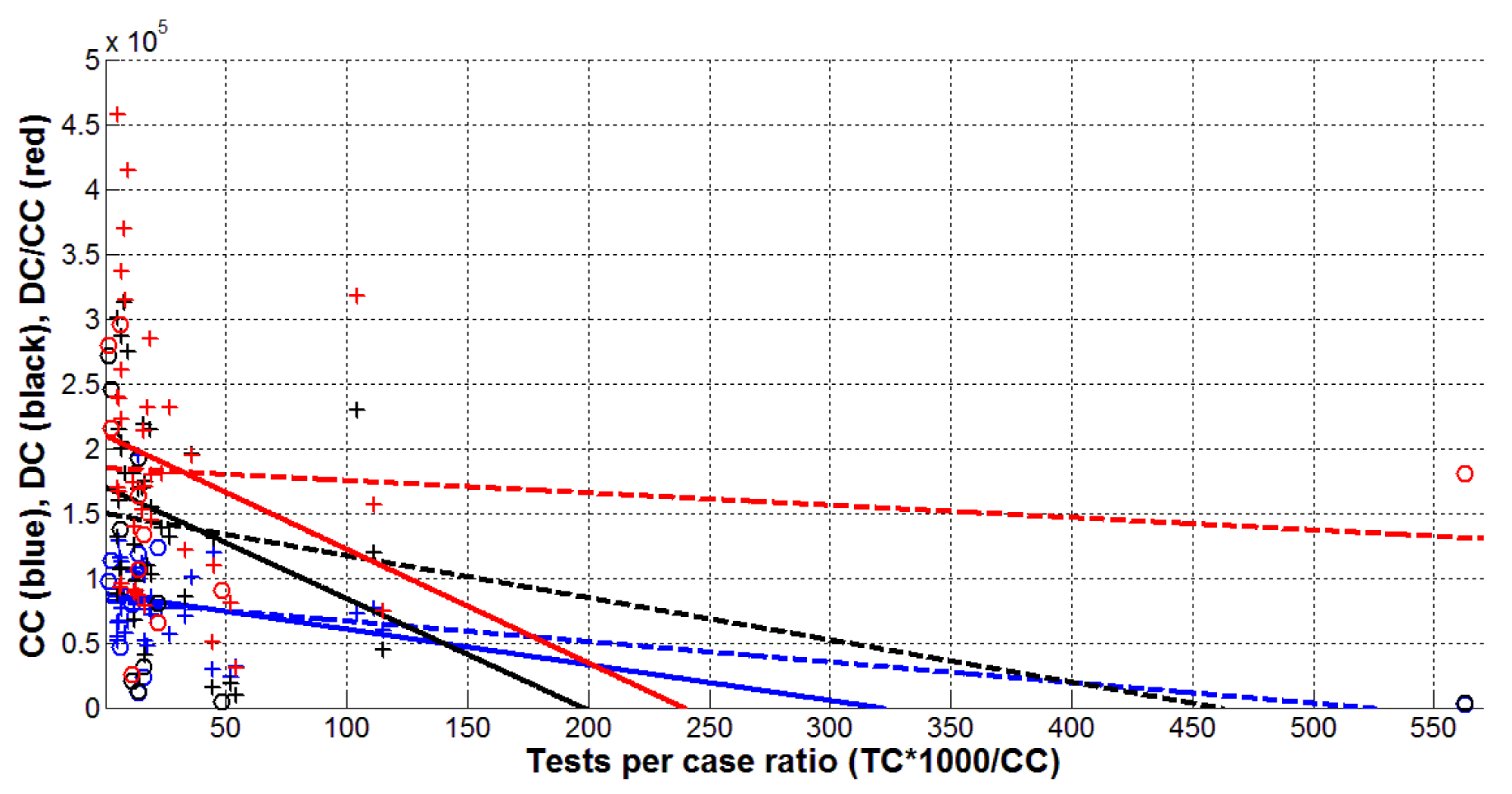
In comparison, the increase of the relative characteristic - number of tests per case ratio (TC*1000/CC) – always diminishes the CC, DC and DC/CC values (see lines in Figure 2). Moreover, visible correlations with TC/CC were revealed for CC and DC values ( $F/F_C(k_1,k_2)<1$ only in the relationship CC versus TC/CC for European countries). This fact allows us to conclude that the increase in the tests per case ratio could stop the pandemic. To calculate the corresponding critical TC/CC values let us put in eq. (1) y = 0 and obtain the corresponding x0 value as follows:

$x_0=-\frac{a}{b}$

Application of formula (3) for 3 cases with $F/F_C(k_1,k_2)>1$ yields the result that new COVID-19 cases in the world could stop when TC*1000/CC > 520 (see: the blue dashed line in figure 2); deaths in the world could disappear at test per case ratio greater than 460 (see the black dashed line); the critical value for the deaths in Europe is TC*1000/CC = 198 (see the black solid line).

Only one country – Australia – exceeded these estimations for the critical values of the tests per case ratio (see last right “circles” in figure 2). The corresponding CC and DC values in this country are very low (see blue and black “circles”). Nevertheless, new cases and deaths occur in Australia. This situation can be explained by a decrease in the number of tests. As of September 1, the daily number of tests per 1,000 population was 10,069 [1]. Taking the corresponding DCC value 48.306 from table 1, we obtain 208.4 as a recent value of the tests per case ratio.

In contrast to the values ​​of DC, the ratio DC/CC does not show any visible correlation with the tests to case ratio TC*1000/CC especially for the complete datasets (in table 2, the corresponding value of the regression coefficient r is -0.0790). This statistical conclusion may seem strange at first glance, but the ratio DC/CC shows how many sick people die. That is, it is a characteristic of the ability of patients to resist the captured strain of the coronavirus and the level of medical care. Therefore, it should not depend on the number of tests performed to identify one infected patient.

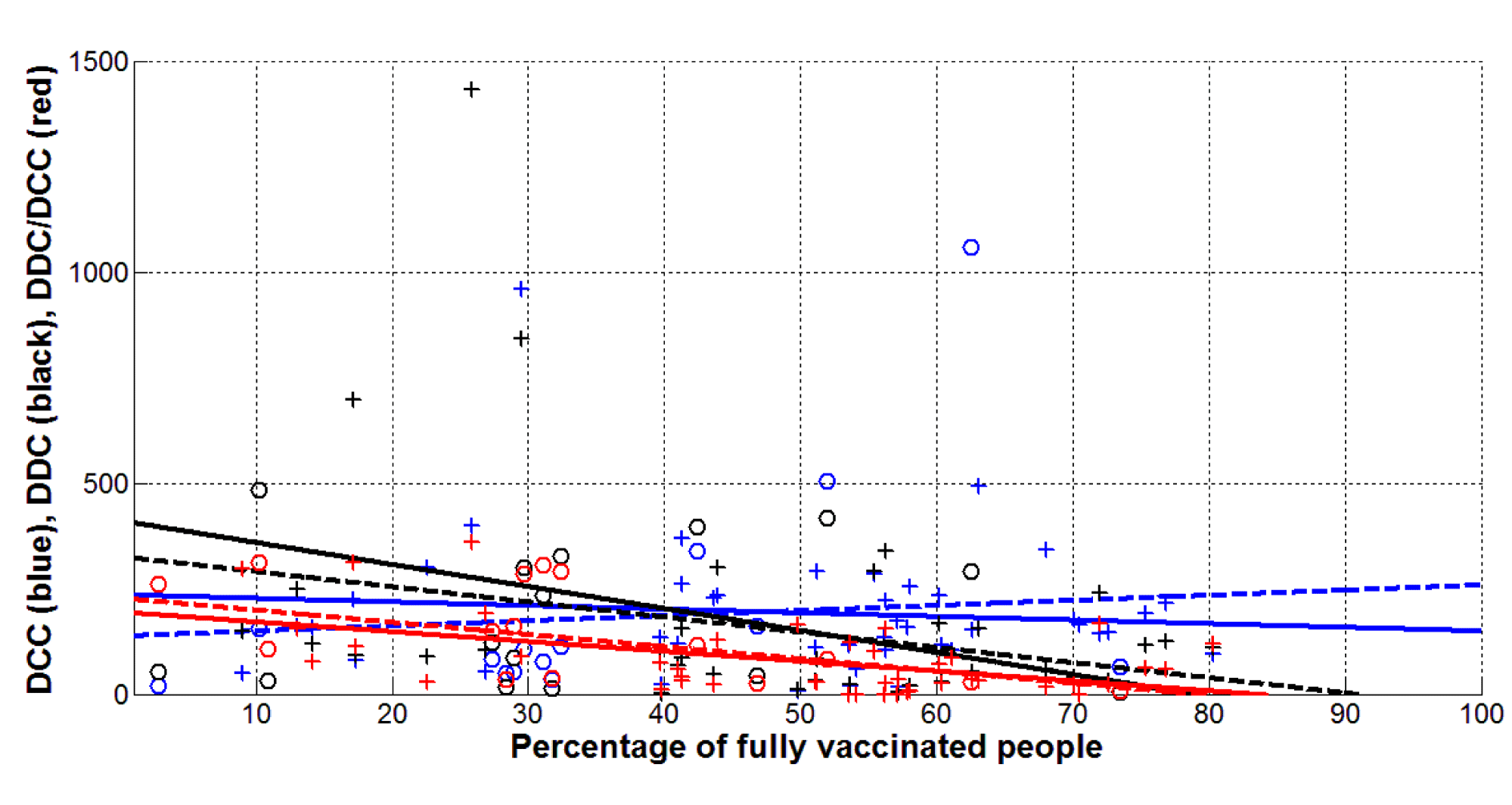
The effect of vaccination levels VC on the daily number of new cases DCC was much unexpected due to the practical lack of correlation. We can see in table 2 the values of the correlation coefficients -0.1004 and 0.1245 for the European and complete datasets, respectively and $F/F_C(k_1,k_2)<<1$ . The same conclusion can be drawn from the best fitting blue lines shown in figure 3. The available statistical data show that new cases will appear even if the entire population of the earth is vaccinated. But vaccination significantly reduces the number of new deaths (see black lines in figure 3) and attitudes of DDC/DCC (red lines). We can see also in table 2 that $F/F_C(k_1,k_2)>1$ for both datasets. Large values of calculated for the relationship DDC/DCC versus VC show that vaccinated infected persons will most likely not die, i.e. the course of the disease will not be very severe.

We can use eq. (3) in order to estimate the critical values of the vaccination level VC when the new deaths cease to appear. Taking the values of a = 4.1071 and b = -0.0521 corresponding to the relationship DDC versus VC (Table 2) we obtain the critical vaccination level 78.8% for the European dataset. For the complete dataset this figure is 90.7%. The black lines in figure 3 illustrate these critical values. The most reliable relationships DDC/DCC versus VC yield the critical values 83.1% and 78.8% for European and complete datasets, respectively (see red lines in figure 3). Looking at table 1, we see that as of September 1, 2021, no European country has reached the appropriate critical level of vaccination 83.1%. The same can be said for other countries and regions shown in table 1.

It should be noted that the vaccination levels listed in table 1 are calculated based on the full volume of populations (including children), so a further increase in VC values ​​(in order to exceed critical figures) requires vaccination of children. Another disadvantage of existing vaccines is their ineffectiveness against new strains of coronavirus, because as mentioned above, new cases will continue to appear even with 100% vaccination. Here is a very illustrative example of Israel, which was experiencing a strong wave in September 2021, despite a fairly high level of vaccination (more than 63.3%). In particular, the daily number of new cases exceeded the values ​​registered before the start of vaccination [4]. The emergence of new cases (even if they are not fatal) increases the likelihood of appearance of new more pathogenic strains, which can dramatically worsen the situation. Therefore, to overcome the pandemic, we should not rely only on vaccination.

The presented statistical analysis shows that vaccinated individuals can become re-infected and are just as dangerous to others as those who have not been vaccinated (since the DCC values do not correlate with the vaccination level). Therefore, the introduction of special passports that remove restrictions for vaccinated persons does not make sense. Having fresh PCR tests can be a more effective pass to crowded places in order to prevent the spread of infection.

Many EU countries are ready to lift all coronavirus restrictions and Denmark has already done this on September 17, 2021 [11]. The obtained results allow us to estimate the risks connected with it. First, as mentioned earlier, even 100 percent vaccination does not save from the emergence of new waves. Unfortunately, the probability of death in the case of infection (daily deaths per case ratio DDC/DCC) remains high due to the fact that the current levels of vaccination are less than the critical values ​​calculated in the previous section.

For example, in Denmark, the vaccination rate VC on September 16, 2021 was 76.38% and 3 deaths caused by coronavirus were registered. Putting this figure into eq. (1) with corresponding values of coefficients a and b for European case from table 2:

$\left(\text{DDC}/\text{DCC}\right)=0.0\text{194 }-\text{ 2}.\text{3335e}-0\text{4}*\left(\text{VC}\right)\text{ (4)}$

we can obtain DDC/DCC = 0.0016. Thus, for every thousand new cases of infection (the number of which may become quite large), approximately 1.6 deaths could be expected in Denmark.

The results obtained in this study do not in any way deny the need for vaccinations. On the contrary, equation (4) shows that the mortality rate can be significantly reduced with a high percentage of vaccinated persons. In the example of Denmark, we see that vaccinations have made it possible to reduce mortality rate DDC/DCC by about 12 times (DDC/DCC = 0.0194 at VC = 0%). But, unfortunately, it will not be possible to completely stop the COVID-19 pandemic with the use of existing vaccines, since DCC values do not correlate with the vaccination level VC.

To discuss the possibilities of complete cessation of the pandemic, let us pay attention to the dependence of CC versus TC/CC for the complete data set shown by the blue dashed line in figure 2. As mentioned earlier, the epidemic can be taken under complete control (CC values ​​are close to zero), if the number of tests per case is high enough (TC*1000/CC > 520).

Indeed, if every detected case is accompanied by testing of many possible contacted persons and isolation of the infected ones, then we have a chance to completely stop the spread of infection. For the case of coronavirus, the number of such tests is quite large. But as the situation in Australia shows, the appropriate level of testing can be achieved (Figure 2). Due to this the CC value in this country is 2193.25 which is much less than the corresponding figures ​​for other countries and regions listed in table 1 (for example, in the whole world, this value is 12.6 times higher).

Hong Kong and mainland China have even lower CC values: 1603.776 and 65.772, respectively (as of September 1, 2021). The test per case ratios were rather high for Hong Kong: 300.8 (January 31, 2020); 222.9 (July 31, 2020); 680.4 (August 31, 2021); all figures were calculated with the use of information about accumulated numbers of tests and cases available in [1]. Thus, at the beginning of the COVID-19 pandemic, the tests per case values ​​were less than critical one, but in the summer of 2021 they exceeded the critical level. Apparently, this allows more or less effective control of the epidemic in Hong Kong at rather low vaccination level. For example, as of September 1, 2021 DCC = 0.738 which is 111 times less than worldwide (Table 1) and VC = 46%.

It seems that in mainland China, many more tests were performed per one laboratory-confirmed case. Unfortunately, the data reported by JHU [1] allows us to calculate only two values 1078 (June 24, 2020) and 1891 (August 6, 2020). Such high levels of testing are likely to have led to complete control of the epidemic in China. The value DCC = 0.019 (September 1, 2021 [1]) is 4312 times lower than worldwide (Table 1).

Increasing the number of tests requires significant costs. But in the periods between pandemic waves (when the daily number of new cases is small), even poor countries can afford to do extensive testing of possible contacts and rapid isolation of infected people. If the number of tests per case everywhere exceeds 520, we will have a chance to stop the COVID-19 pandemic.

A simple statistical analysis of the daily number of new cases (DCC) and deaths (DDC) per capita showed that vaccination can significantly reduce the likelihood of deaths (DDC/DCC values). However, existing vaccines do not prevent new infections, and vaccinated individuals can spread the infection as intensely as unvaccinated ones. Therefore, it is too early to lift quarantine restrictions in Europe and most other countries.

The constant appearance of new cases due to re-infection increases the likelihood of new coronavirus strains, including very dangerous ones. As existing vaccines are not able to prevent this, it remains to increase the number of tests per registered case (TC*1000/CC values). Statistical analysis showed that if the critical value of 520 is exceeded, one can hope to stop the occurrence of new cases.

1. COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU).  https://bit.ly/3FKlnh3
2. Nesteruk I, Rodionov O. The impact of demographic factors on the accumulated number of COVID-19 cases per capita in Europe and the regions of Ukraine in the summer of 2021. medRxiv, July 2021. doi: 10.1101/2021.07.04.21259980.
3. Nesteruk I, Rodionov O, Nikitin AV. The impact of seasonal factors on the COVID-19 pandemic waves. medRxiv, August 2021. doi: 10.1101/2021.08.06.21261665.
4. Nesteruk I. Influence of Possible Natural and Artificial Collective Immunity on New COVID-19 Pandemic Waves in Ukraine and Israel. Explor Res Hypothesis Med. 2021. doi: 10.14218/ERHM.2021.00044.
5. Nesteruk I. COVID-19 pandemic dynamics. Springer Nature. 2021. doi: 10.1007/978-981-33-6416-5.
6. Nesteruk I. Visible and real sizes of new COVID-19 pandemic waves in Ukraine Innov Biosyst Bioeng. 2021;5(2):85-96. doi: 10.20535/ibb.2021.5.2.230487.
7. Nesteruk I. Detections and SIR simulations of the COVID-19 pandemic waves in Ukraine. Comput Math Biophys. 2021;9:46-65. doi: 10.1515/cmb-2020-0117.
8. Draper NR, Smith H. Applied regression analysis. 3rd ed. John Wiley; 1998. 
9. https://onlinepubs.trb.org/onlinepubs/nchrp/cd-22/manual/v2appendixc.pdf
10. Nesteruk I. Comparison of the First Waves of the COVID-19 Pandemic in Different Countries and Regions. In book: COVID19 pandemic dynamics. Springer Nature, 2021. https://bit.ly/3DShN46
11. https://time.com/6096807/denmark-covid-19/