Biology Group . 2022 May 13;3(5):537-546. doi: 10.37871/jbres1476.
Interactions b/w Collagen and Polylactic-Acid Molecular Models Due to DFT Calculations
Kazunaka Endo1*, Megumi Fuse2 and Nobuhiko Kato3
2Department of Liberal Arts (Chemistry), School of Dentistry Matsudo, Nihon University, Matsudo Chiba, Japan
3ASTOM R&D Koishikawa, Bunkyo-ku Tokyo, Japan
- Type I collagen
- Polylactic acid
- DFT
- MO
- Inter-and Intra-H-Bond
Abstract
Collagen and Polylactic Acid (PLA) as biomaterials in the tissue engineering have been investigated for the structure and function in considerably large progress. From a viewpoint of its electronic structures in the subnano-meter range, we investigate the bonding nature for five models of the type I collagen, PLA models and the bimolecular interaction between the models by using Density Functional Theory (DFT) calculations with Frontier MO theory. In order to confirm the accuracy of the models, we compare the simulated IR and C1s X-ray photoelectron spectra with experimental results. Especially, the interaction between PLA and (AspHypGly)-collagen models was obtained as the chemical bond energy (1540 kJ/mol), and the results of PLA-other four collagen bimolecular models were given as intermolecular bond energies of 30 ∼ 81 kJ/mol. The intermolecular interaction is due to inter-H-bond of –OH---O=, -NH---O=, and –CH---O= functional groups, respectively, using MO calculations.
Introduction
Collagen and polylactic acid scaffolds play important roles as biomaterials in tissue engineering. The collagen molecules represent the most abundant protein building block in the human body, where they provide primarily mechanical stability, elasticity, and strength to connective tissues such as tendons, ligaments, and bone. Polylactic Acid (PLA) is a well-known synthetic polymer which has great potential for use as a scaffold material because of its slow rate of resorption [1]. The surface properties of the scaffold are responsible for the adsorption of proteins and other biological molecules which regulate the cell’s response such as adhesion, migration, proliferation and other material-protein interactions [2-5]. PLA which degrades into innocuous lactic acid is used as medical implants in the form of anchors, screws, plates, pins, rods, and as a mesh [6]. Depending on the exact type used, it breaks down inside the body within 6 months to 2 years. This gradual degradation is desirable for a support structure, because it gradually transfers the load to the body (e.g. the bone) as that area heals [7].
A distinctive feature of collagen is the regular arrangement of amino acids in each of the three chains of the collagen subunits. The sequence often follows the pattern glycine (Gly)-proline (Pro)-X or Gly-X-hydroxy-proline (Hyp), where X is any of various other amino acid residues [8]. Pro or Hyp constitute about 1/6 of the total sequence. With glycine accounting for the 1/3 of the sequence, this means approximately half of the collagen sequence. The Gly-Pro-Hyp triplet fits well into the triple helix structure because it has relatively small side chains, however other residues with more substantial side chains can still be accommodated by directing the side chains away from the central axis. They are easily accessible to the surrounding solvent and allow for polar and charged side chains to form additional (water mediated) intra-molecular bridges via H-bonding [9-11]. The side chains are also accessible to other molecules, biominerals, or proteins in the biological environment. Hence, the identities of the residues at the X and Y positions to some extent govern the interaction properties of the collagen molecule. Regions along the collagen triple helix with a high degree of substitution of Pro and Hyp for charged and hydrophobic residues often function as binding sites.
As we know, there are three interesting studies of ‘genipin-collagen immobilization of Polylactic Acid (PLA) fibers’ [12], ‘poly (lactic-co-glycolic acid) interactions with collagen, [13], and ‘Surface characterization, collagen adsorption and cell behaviour on poly (L-lactide-co-glycolide) ‘[14]. They indicated compatiblity of interaction with PLA and collagen, and however we think there is no study until now from nanoscopic interaction viewpoints. Then, from a fundamental standpoint as well as for designing biomaterials, it is often important to obtain the information on sub-nanoscale from quantum chemical field. In the two decades, the software performance of the quantum chemical calculation developed remarkably with rapid progress of the hardware capacity of the computer, and we are, then, able to perform the considerable precise calculation about the electronic state of the biomaterials.
In this work, we demonstrate electronic structure and bonding calculations of five amino-residence models [Proline-Hydroxyproline-Glycine(ProHypGly){PHG}, Proline-Arginine-Glycine(ProArgGly) {PAG}, Glutamine-Hydroxy- Proline-Glycine(GluHypGly){GHG}, Proline-Lysine-Glycine(ProLysGly) {PLG}, Asparagine-Hydoxyproline-Glycine (AspHypGly){AHG}] for the type I collagen and PLA model using the Density Functional Theory (DTF) method [15] with Frontier molecular orbital theory [16]. For PLA, type I five collagen models, and the bimolecular model molecules, the intra- and inter-hydrogen bonding energies are estimated from empirical MO method [17,18].
Computational Details
Individual models for PLA and collagen five amino-residences
The initial geometric structures for model molecules of Polylactic Acid (PLA) (Total atoms = 30, Total electrons = 124) and type I collagen five amino-residences {Proline-Hydroxyproline-Glycine (PHG) (Total atoms = 38, Total electrons = 144), Proline-Arginine-Glycine (PAG) (total atoms=47, total electrons=168, charge = +1), Glutamine-Hydroxyproline-Glycine (GHG)(total atoms=39, total electrons=160, charge = −1), Proline-Lysine-Glycine (PLG) (total atoms=45, total electrons=154, charge = +1), Asparagine-Hydoxyproline- Glycine (AHG) (total atoms=36, total electrons=152, charge = −1)} were optimized at a semiempirical PM7 method [17,18]. Furthermore, we performed the second geometry-optimization with B3LYP/ TZVP level in GAUSSIAN 09 program [15] by using the Cartesian coordination from the initial geometry-optimization. Figure 1 shows molecular models for PLA, and type I collagen five amino-residences. In order to simulate IR and C1s XPS spectra of PLA and the five collagen model molecules, we performed DFT SCF calculations at the B3LYP/6-31G(d, p) level with the keyword of ‘Freq.’ Thus, we obtained the harmonic frequencies of their model molecules at the optimized geometries. We have cited the experimental IR spectra [12,19] of PLA and type I collagen films, respectively. For C1s XPS analysis, we used SCF converged energies values of the PLA and collagen model molecules as the electron binding energies using Koopmans theorem. The calculated intensities of C1s XPS were obtained from abundance ratios of fuctional groups for the PLA and collagen model molecules. In the case of experimental spectra of the C1s XPS for PLA and collagen substances, we referred from the manuscript [12,14].
a) Interaction system between PLA and type I collagen model molecules
We consider the bimolecular interaction systems between PLA and type I collagen five amino-residences models. The initial geometric structures for bimolecular systems were also optimized at a semiempirical PM7 method [17]. Furthermore, we performed the second geometry- optimization with B3LYP/6-31G (d,p) level in GAUSSIAN 09 program [15] by using the Cartesian coordination from the initial geometry-optimization. In table 1, converged total energies of five bimolecular systems were indicated with sum energies of individual models for PLA and collagen five amino-residences. Therefore, in the table, we could calculate the interaction energies of bimolecular systems between PLA and five collagen models.
| Table 1: Geometry-optimization energies for PLA, and Collagen mlecular models (PAG, GHG, PHG, PLG, AHG), and their interaction energies. |
| Molecular models energies (hartree) |
| individual sum bimolecular stabilization |
| (PLA+collagen-model) system energy( kJ/mol) |
| PLA -878.008 |
| *(HartreeFock MO) -873.086 |
| Collagen mlecular models |
| PAG(ProArgGly) -1064.521 |
| GHG(GluHypGly) -1083.808 |
| PHG(ProHypGly) -933.889 |
| PLG(ProLysGly) -954.983 |
| AHG(AspHypGly) -1044.503 |
| *(HartreeFock MO) -1038.490 |
| PLA-PAG -1942.529 -1942.549 0.020 (52.5 kJ/mol) |
| PLA-GHG -1961.816 -1961.827 0.011 (28.9 kJ/mol) |
| PLA-PHG -1811.897 -1811.923 0.026 (68.3 kJ/mol) |
| PLA-PLG -1832.991 -1833.021 0.030(78.8 kJ/mol) |
| PLA-AHG -1922.511 -1923.089 0.578(1540 kJ/mol) |
| *(HartreeFock MO) -1911.576 -1912.146 0.569(1490 kJ/mol) |
b) Intra- and inter-H bonding energies of PLA, type I five collagen, and the bimolecular model molecules>
For PLA, type I five collagen, and the bimolecular model molecules, we estimated the intra- and inter-hydrogen bonding energies with 1SCF calculation of empirical MO method [18] by using the Cartesian coordination from the second geometry-optimization in GAUSSIAN 09 program. The bond enegy was obtained as the two-center bond-energy using keywords “(AM1 XYZ 1SCF VECTORS ALLVEC BONDS ENPART)” in Winmopac sofware [18] calculations. The scaling factor (0.280) was evaluated as the averaged value of the two-center bond-energy divided by the experimental bond-dissociation energy [20] for each chemical bond in table 2. The energy values were used in our previous works [21-23]. In this work, we also use the value in order to perform intra- and inter-H bonding energy calculations of PLA, type I five collagen models, and the bimolecular model molecules.
| Table 2: Experimental bond-dissociation and calculated bond energies. | ||
| Bond Experimental | Bond- Energies* Dissociation Energies |
Bond Evaluated from Am1 Method |
| Ev | Ev | |
| C−C | 3.2~4.4 | 3.2~4.2 |
| C=C | 6.3 | 5.4~6.6 |
| C~C | 8.7 | 8.9 |
| C−O | 3.7 | 3.7~4.0 |
| O−CO | 4.8 | 4.3~4.6 |
| C=O | 7.7~7.8 | 6.8~7.1 |
| C−F | 4.1~5.4 | 4.6~4.8 |
| C−Cl | 2.9~4.1 | 3.0~3.5 |
| C−H | 3.7~4.9 | 3.3~3.5 |
| *The values were obtained from (two-center bond-energies by AM1 method) × 0.280. # (#The scaling factor was evaluated as the averaged value of the two-center bond-energy divided by the experimental bond-dissociation energy for each chemical bond) |
||
Results and Discussion
Since it is lacking in the fundamental understanding of its electronic structures in the subnano- meter range, we investigate the electronic structure and bonding nature for five models of the type I collagen, PLA, and the interaction between collagen and PLA models using the DTF method. In order to clarify the accuracy of collagen and PLA models, we compare simulated IR and XPS spectra of collagen and PLA models with the experimental ones. Furthermore, we describe nanoscopic interaction types between collagen and PLA models using Frontier molecular orbital theory.
a) IR and C1s XPS for PLA and collagen five amino-residences
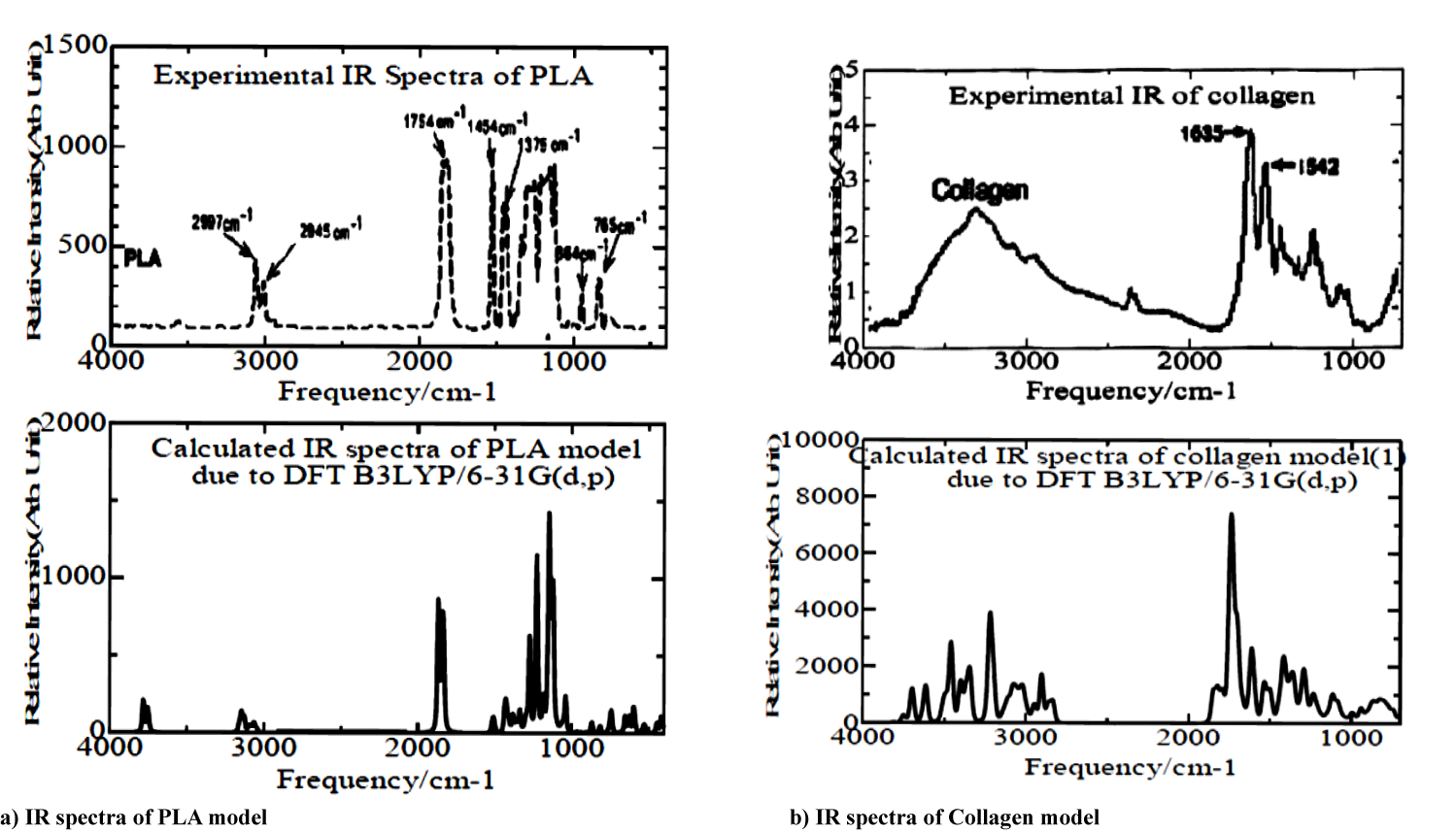
We indicated simulated and experimental vibrational frequencies for PLA and collagen model molecules in figures 2a & 2b and table 3. In the figure, simulated IR spectra correspond considerably well to the experimental ones. In the case of the PLA model, experimental broader spectra in the range of 1000 ∼ 1300 cm-1 in figure 2a show bending vibrations of functional (-CH2, -OH, -C=O) groups, and experimental two peaks around at 1375 and 1474 cm-1 appear to be bending vibrations of -CH2 groups. Simulated doublet peaks between 1835 and 1866 cm-1 in the figure correspond to the experimental one at 1754 cm-1 due to the streching vibration of -CO group, and smaller theoretical doublets in the range of 3050 ∼ 3160 cm-1 are owing to experimental similar ones at 2845 and 2987 cm-1.
| Table 3: Calculated IR frequencies of PLA and collagen models with experimental ones. | |
| Streching Vibrations Model Molecule Experimental Functional Group Range(cm-1) Range(cm-1) |
Bending Vibrations Functinal Model Molecule Experimental Group Range(cm-1) Range(cm-1) |
| -CH, -CH2, -CH3 P LA (3050-3160) 2850-3050 -C=O PLA (1835- 1866) 1700-1750 -OH AHG(3611) 3200-3550 -NH AHG(3197, 3366) 3300-3400 -C=O AHG(1738, 1749, 1848) 1700-1750 -CH, -CH2 AHG(3015,3036,3072, 3078,3081) 2850-3000 -NH PAG(3220,3341,3457,3490 3627,3699,3750) 3200-3500 -CH PAG(2951,3015,3029,3058, 3106,3123) 2850-3050 -C=O PAG(1695, 1702, 1743,1825) 1700-1750 -CN PAG(1537,1615,1665,1695, 1702,1743) 1640-1690 -NH PLG(3425,3428,3490,3528) 3200-3500 -CH PLG(2958,3018,3040,3059, 3069,3120,3124) 2850-3050 -C=O PLG(1681, 1729,1821) 1700-1750 -CN PLG(1524,1534) 1640-1690 NH GHG(3400)) 3200-3500 -CH GHG(2833,2900,2996,3001, 3003,3011,3021,3051,3082) 2850-3050 -C=O GHG(1725, 1733, 1742,1845) 1700-1750 -OH PHG(3697) 3200-3550 -NH PHG(3487,3508) 3200-3500 -CH PHG(2942,3017,3029,3039,3054, 3077,3102,3111,3119) 2850-3050 -C=O PHG (1751, 1791,1812) 1700-1750 -CN PHG (1148,1413,1418,1592) 1640-1690 |
-CH2 PLA (1350,1353, 1386, 1439,1445,1454,1469) 1350-1470 -CH2,-OH, PLA(1122,1125,1145, -C=O 1226,1273) 1200-1300 -NH2, CH2 AHG(1611,1689) 1500-1600 -CH2, -NH2 AHG(1230,1240) 1200-1300 -CH2,-C=O AHG(1353,1356,1366) 1350-1450 -NH PAG(1493,1537,1615,1665, 1695,1702,1743) 1500-1600 -CH PAG(1493,1535,1537) 1380-1465 -NH PLG(1524,1534,1593,1623, 1661,1681,1729) 1500-1600 -CH,-CH2 PLG(1109,1380) 1380-1465 - NH GHG(943, 1602,1635) 1500-1600 -CH GHG(1233,1296,1374,1375, 1392,1418,1500,1602) 1380-1465 -NH PHG(1291,1418,1427,1791) 1500-1600 -CH PHG(1291,1413,1418,1427) 1380-1465 |
For collagen models, we showed the calculated smaller broader complicated peaks (2900 3050 cm-1) and intermediate strong peaks (3200∼3550 cm-1) due to streching vibrations of -CH, and (-NH, -OH) groups, respectively, in the lower plot of figure 2b. The simulated spectra seem to agree in the experimental broader curve in the range of 2800 ∼ 3800 cm-1 in the upper plot of figure 2b. In many experimental IR peaks between 1000 and 1750 cm-1 in figure 2b, the intensive peak at 1635 cm-1 depends on calculated one at 1750 cm-1, and other resident experimental peaks are due to bending vibrations of functional (-CH2, -OH, -C=O) groups.
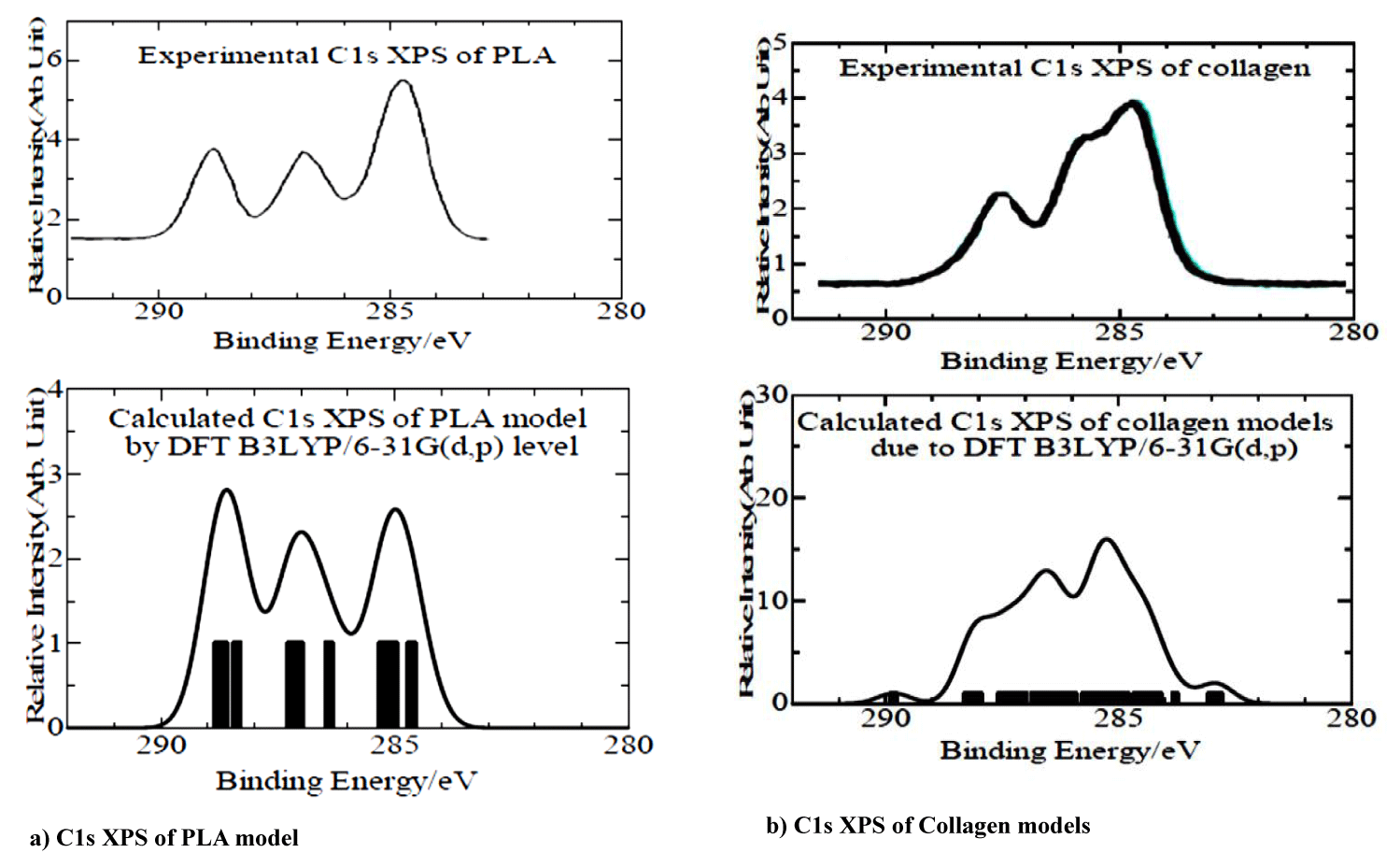
As described in Computational Details, we used the electron binding energies of the PLA and collagen model molecules due to the Koopmans theorem from SCF converged energies values of the model molecules. In table 4, simulated C1s Core-Electron Binding Energies (CEBE)’s of the model molecules were given in the relative to -CH, and -CH2 functional groups as 285.0 eV. In the table, we gave the shifted values from difference between SCF converged energies values of the model molecules and 285.0 of -CH, and -CH2 functional groups, although it is characteristic that the shifted values were amounted as 12.2 and 11.2 eV for the total charge (-1) of model molecules in the type I of collagen. In figures 3a & 3b, we showed simulated C1s XPS of PLA and collagen models using the CEBEs in table 4 with experimental ones, respectively. Calculated C1s XPS in both PLA and collagen cases are in considerably good agreement with experimental ones. Thus, it concludes that our PLA and collagen model molecules are reasonable to analyze the electronic states of individual ones and the interaction bimolecular system.
| Table 4: C1s Core-electron Binding Energies of PLA and Collagen models. |
| Experiment Calculated(eV) |
| Functional (eV) PLA AHG PAG PLG GHG PHG |
| Group |
| C-H 285.0 (284.6,285.0,285.2) (285.0) (284.2,284.4, 250.0,285.3) (284.2,284.3285.0,285.3,285.5) (284.2,285.0,285.5) (284.7,285.0,285.2) |
| C-O-C 286.5 (286.4,287.0,287.2) |
| C-OH 286.6 (287.2,287.2) 286.9 |
| -C=O 287.9 (288.4,288.6,288.7) (288.4,288.5,288.8) 287.3 287.4 287.5 |
| -C(=O)-O- 289.0 290.3 288.7 |
| -C-NH 285.9 (286.7,286.8, (285.5,285.5, (285.6,285.8,286.5, (285.9,286.0, (285.4,285.7, 286.3, |
| 287.4,287.6) 286.4,286.5,286.7) 286.8, 287.4) 286.4, 286.5) 286.4, 286.5) |
| -C(=O)-NH 288.1 (289.3,290.2) (287.9,288.0) (288.3,288.3) (288.0,288.2) (287.7,288.2) |
| -N-C(-N)-N 289.8 |
| Shifted value* 7.5 12.2 5.0 4.9 11.2 7.6 |
| *C1s CEBEs were given in the relative to –CH, and –CH2 functional groups as 285.0 eV. |
b) Individual MO calculation analysis of PLA and type I collagen model molecules
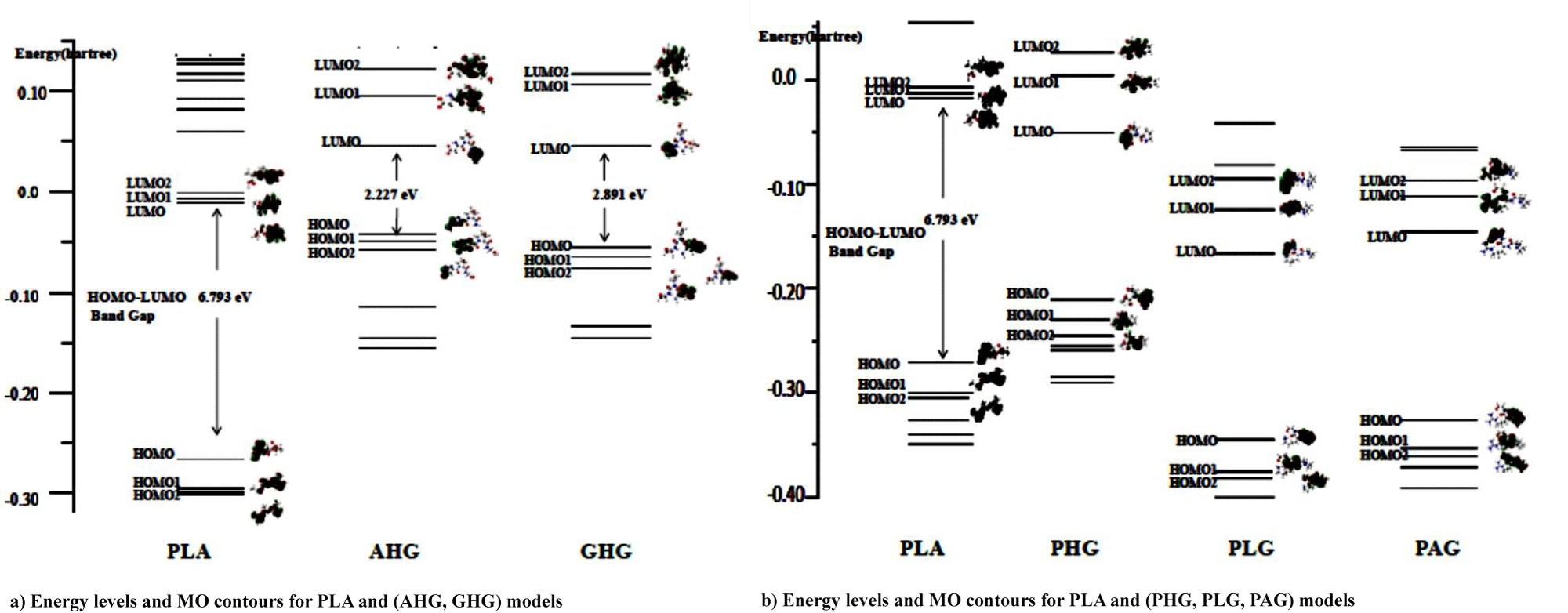
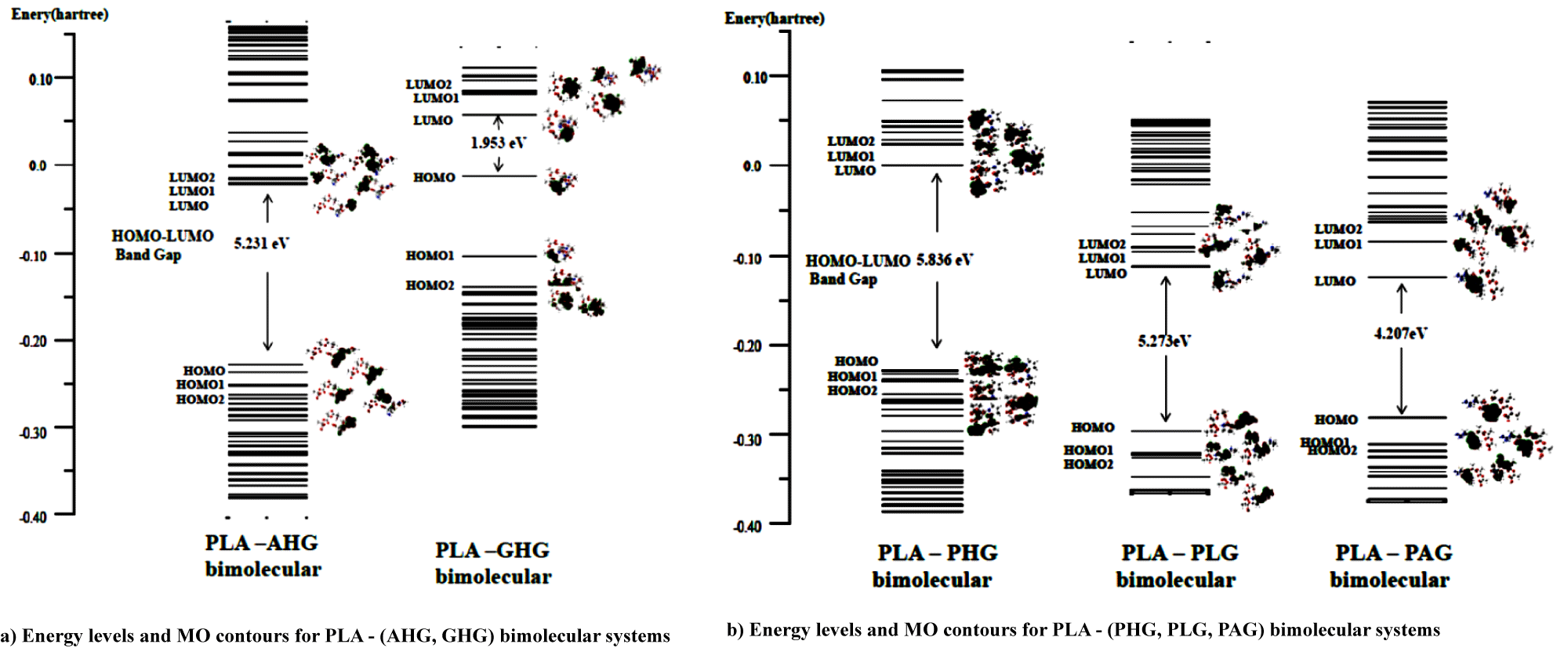
Figures 4a & 4b shows MO energy levels (with hartree unit) of PLA and collagen models at the ground electronic state from the DFT calculations. In the figure, in order to discuss the interaction system on the Frontier MO theory [16], we ploted the MO contours for three MO levels lower and upper from the Highest Occupied (HOMO) and Lowest Unoccupied (LUMO) MOs, respectively for the PLA and five collagen model molecules. For MO contours of PLA in figure 4, three HOMO, HOMO1, and HOMO2 (HM, HM1, HM2) levels for the PLA model were indicated with bonding orbitals owing to –C=O and –C–O–C functional groups, severally, while the LUMO, LUMO1, and LUMO2 (LM, LM1, LM2) were written with the anti-bonding orbitals of the groups. In table 5, we showed MO contour functional groups for occupied (HM, HM1, HM2) and unocupied (LM, LM1, LM2) orbitals of PLA and (AHG, GHG) collagen models.
| Table 5: MO Contour functional groups for (HM, HM1, HM2) and (LM, LM1, LM2) of PLA and cllagen models. |
| Molecular HOMO HOMO1 HOMO2 ; LUMO LUMO1 LUMO2 |
| Model Bonding orbitals Anti-bonding orbitals |
| −C=O, −C−O−C C=O, −C O−C PLA −C=O, −C−O−C −C=O, −C−O−C −C=O, −C−O−C C=O, C−O−C |
| two −C=O −C=O AHG two −C=O, −C=N− C=N, −C=O Two −C=O −C=O, two −C=N− |
| two −C=O −C=O GHG two −C=O −C=N−, −C=O(in hydroxy-pyrrolidine) two −C=O −C=N−, −C=O(in hydroxy-pyrrolidine) |
| pyrrolidine −C=O, −N=C PHG −C=O, hydroxy-pyrrolidine −N=C=O, hydroxy-pyrrolidine −C=N−C, hydroxy-pyrrolidine −N=C=O, hydroxy-pyrrolidine |
| −N=C=O, pyrrolidine −C=O PLG two −N=C=O −C=O, two −N=C=O −C=O, two −N=C=O, pyrrolidine −C=O, two =N−C |
| Pyrrolidine −C=O PAG two −N=C=O –C=O, −N=(C(=N)=N two −N=C=O, pyrrolidine –N−C=O, −N=(C(=N)=N |
For AHG collagen model in table 5, MO contours of the occupied HM, HM1, and HM2 levels are due to bonding orbitals of the two –C=O, (two –C=O, −N−C), and two –C=O groups, respectively. On the other hand, MO figures of unoccupied LM, LM1, and LM2 result in anti-bonding orbitals of –C=O, (−C=N−, –C=O), and (–C=O, two −C=N−) functional groups, severally, the last two groups involve the hydroxy-pyrrolidine ring. In the case of GHG model in the table, MO contours of the occupied HM, HM1, and HM2 levels are owing to bonding orbitals of the two –C=O, groups in three occupied MOs. However, MO figures of unoccupied LM, and (LM1, LM2) show with anti-bonding orbitals of –C=O, and (−C=N−, and –C=O in hydroxy-pyrrolidine ring) groups, respectively. It is characteristic in figure 4a that the energy gap of HOMO and LUMO for PLA model is 6.8 eV, while the gaps of AHG and GHG collagen models give 2.2 and 2.9 eV. The gaps of two collagen model molecules are considered as semiconductor-like ones.
In figure 4a energy levels of unoccupied LM, LM1, LM2 for PLA model approach to the levels of occupied HM, HM1, HM2 for AHG and GHG collagen models, and thus electrons on the occupied orbitals (HM, HM1, HM2) for the collagen models are able to transfer to unoccupied orbitals (LM, LM1, LM2) of PLA model in the bimolecular interaction system from the Frontier MO theory. The result for bimolecular interactions between PLA and (AHG and GHG) collagen models is shown in figures 5a & 5b. In the figure, energy gap between HOMO and LUMO for the PLA-AHG bimolecular system is 5.2 eV, and then we can call the gap value as an organic insulator. On the other hand, the gap for the PLA-GHG system amounts to 2.0 eV as a semiconductor-like gap. The gap difference between PLA-AHG and PLA-GHG systems is considered to be due to the distribution of frontier MO figures for the system in figure 4a. In the former bimolecular system, the distributions of (LM, LM1, LM2) orbitals of PLA model are different from those of (HM, HM1, HM2) orbitals for AHG. However, the distributions of (LM, LM1, LM2) orbitals of PLA model are similar to those of (HM, HM1, HM2) orbitals for GHG.
For figure 4b, the gaps of PHG, PLG, and PAG collagen models indicate values of 4.4~4.9 eV which correspond to the organic insulators. In table 5, we also showed MO contour functional groups of occupied (HM, HM1, HM2) and unocupied (LM, LM1, LM2) orbitals for the PHG, PLG, and PAG collagen models with AHG, and GHG models. Therefore, we omitted the explanation for the functional groups of PHG, PLG, and PAG collagen models.
In figure 4b, we can estimated the difference energy between HOMO of PLA and LUMO of PHG as 6.0 eV, while the differences between HOMO of PLA and LUMOs of (PLG, PAG) as (3.0, and 3.3) eV, respectively. Then, electrons on occupied orbitals (HM, HM1, HM2) of the PLA model are able to transfer to unoccupied orbitals (LM, LM1, LM2) of (PLG, PAG) models better than the occupied orbitals of PLA model do the unoccupied orbitals (LM, LM1, LM2) of PHG model from the Frontier MO theory. Therefore, it can be seen in figure 5b that the HOMO-LUMO energy gaps of PLA-(PLG, PAG) bimolecular systems are much less as values of (5.3 and 4.3 eV) than the gap of PLA-PHG interaction system obtained as the result of 6.8 eV.
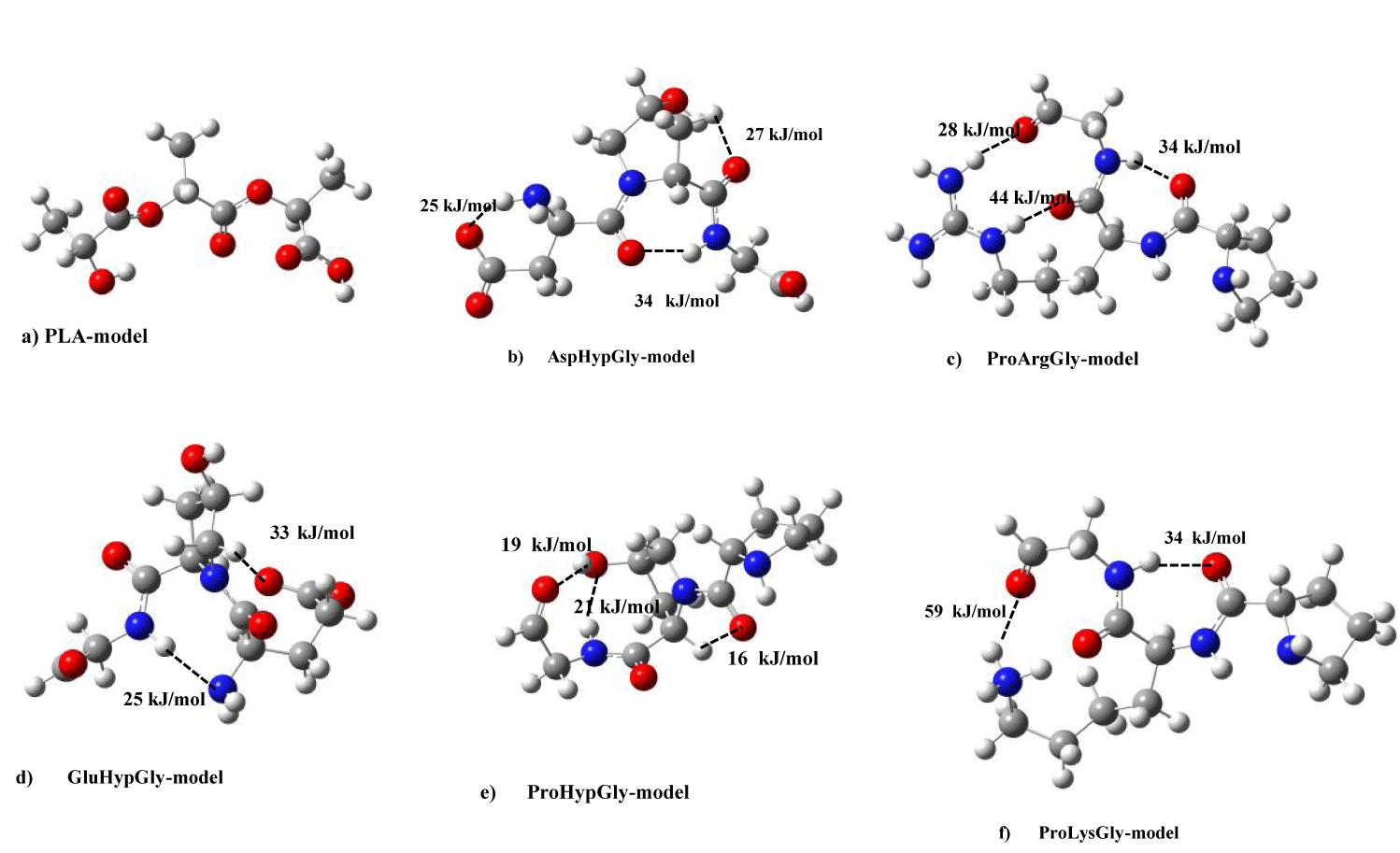
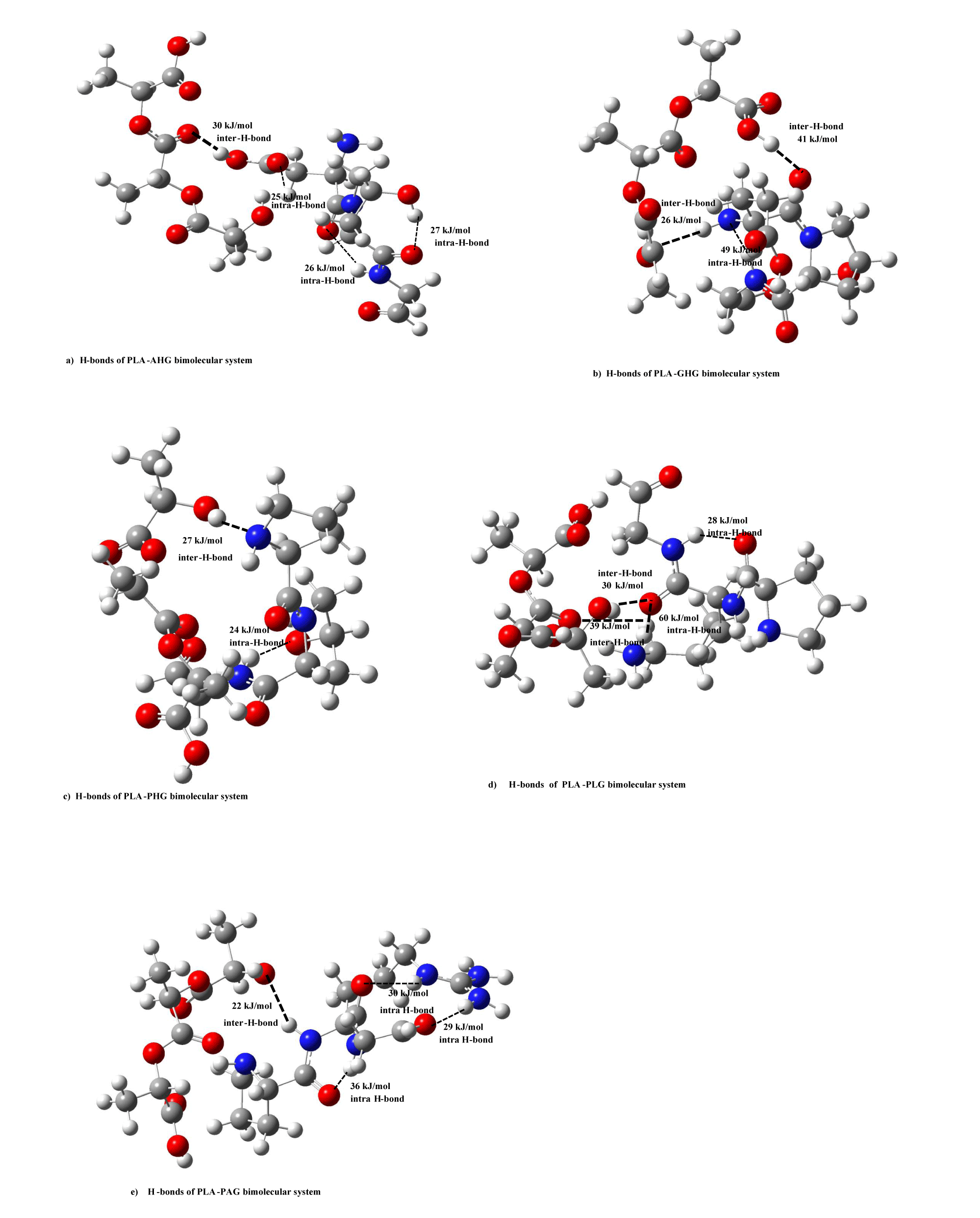
Here, let’s discuss intra-hydrogen (H)-bond energies of PLA and type I collagen model molecules. In figure 1, there is no strong intra-H-bonding for PLA model. In the figure, we showed intra-H-bond energies of five collagen (AHG, PAG, PLG, GHG, and PHG) models deriving collagen helices. In the AHG model (Figure 1b), the energies of three (-NH---O-, -CH---O=, and -NH---O=) functional groups were estimated as 25, 27, and 34 kJ/mol, while three functional (-NH---O=) groups also shown as 28, 34, and 44 kJ/mol for PAG model (Figure 1c). In the case of PLG, and GHG models in figure 1d & 1e, two (-NH---O=) groups have 34 and 59 kJ/mol H-bond energies, and (-NH---N-, -CH---O=) functional ones are 25 and 33 kJ/mol, respectively. For the PHG model, we are able to give intra-H-bond energies as 16, 19, and 21 kJ/mol in -CH---O=, -OH---O=, -NH---O- groups, separately.
c) Bimolecular interaction system between PLA and type I collagen model molecules
We commenced investigating bimolecular interaction system between PLA and type I collagen model molecules from sub-nanoscopic stand-points, since compatiblity of interaction with PLA and collagen was already indicated in three studies [12-14]. In table 1, we showed converged total energies of five bimolecular systems with sum energies of individual models for PLA and collagen five amino-residences. In the table, stabilization energies in the ranges of 30 ∼ 81 kJ/mol were shown as reasonable intermolecular interaction energies [24] for bimolecular systems between PLA and four collagen (PAG, GHG, PHG, PLG) models, although the energy (1540 kJ/mol) of PLA-AHG collagen model is a chemical bonding one, and the result as an intermolecular interaction energy is estimated too large. The estimated value was obtained in similar result (1490 kJ/mol in table 1) from the Hartree-Fock MO calculation ((RHF or UHF)/6-31G(d,p)) in GAUSSIAN 09 program. Therefore, we think there may be a special bimolecular complex which has chemical bond energy.
In order to clarify the nature of stabilization energies between PLA and collagen model molecules, we calculated inter-hydrogen (H)-bond energies of PLA and type I collagen model molecules. In figures 6a-e, we drew inter-H-bond energies between PLA and five collagen model (AHG, PAG, PLG, GHG, PHG) molecules. For PLA-AHG bimolecular system (Figure 6a), we found-out an inter-H-bond (-OH---O=) group of 30 kJ/mol, and in the case of PLA-(GHG, PHG)-bimolecular sytems (In figure 6b,c), in the former interaction type, there are two inter-H-bonds (-C-O---O=, -N-H---O=) groups of (41, 26) kJ/mol, and in the latter PLA- PHG bimolecular system, we are able to give an inter-H-bond of –OH---NH group as 27 kJ/mol. In PLA-PLG interaction system (Figure 6d), two inter-H-bonding groups were shown as (-OH---O=, -CH---O=) values of 30, 39 kJ/mol, and for PLA-PAG bimolecular system (Figure 6e), we described an inter-H-bond of (-NH---O-) value as 22 kJ/mol. These inter-H-bond enegies of the bimolecular types between PLA and five collagen models are comparable to stabilization energies of the systems without PLA-AHG bimolecular type by using abinitio MO calculations, and thus the nature of the intermolecular interaction can be considered to be due to the inter-H bond between PLA and four collagen models.
Even in PLA and five collagen model bimolecular types, we estimated intra-H-bond for five collagen models in figures 6a & 6e as follows: For PLA-AHG system, there are three intra-H-bonds for (-CH---O=, -NH---O=, -OH---O=) groups of 25, 26, 27 kJ/mol, severally, in AHG model molecule in figure 6a. In the case of PLA-(GHG, PHG)-bimolecular systems in figures 6b & 6c, we gave an intra-H-bond (-NH---N-) group of 49 kJ/mol, and an intra-H-bond of (–NH---O-) group as 24 kJ/mol, respectively. In PLA-(PLG, PAG) bimolecular systems, the former case (Figure 6d) has two intra-H-bond (-NH---O=, -NH---O=) groups of 28, 60 kJ/mol, and the latter one (Figure 6e) is composed of three intra-H-bond groups as 30, 29, 36 kJ/mol.
Conclusion
We performed this work from the fundamental understanding of its electronic structures in the subnano-meter range. The results of electronic structure and bonding nature for five models of the type I collagen, PLA model, and the bimolecular system between PLA and collagen models were performed by using DFT calculations.
In order to clarify the accuracy of collagen and PLA models, in comparison of simulated IR and XPS spectra of collagen and PLA models with the experimental ones, we obtained reasonable results: Calculated IR spectra and C1s XPS in both PLA and collagen cases are in considerably good agreement with experimental ones.
We determined MO energy levels (with hartree unit) of PLA and collagen models at the ground electronic state from the DFT calculations. In order to discuss the interaction system on the Frontier MO theory, we ploted the MO contours with three MO levels lower and upper from the highest occupied (HOMO) {as HM, HM1, HM2} and lowest unoccupied (LUMO) MOs{as LM, LM1, LM2}, respectively, for the PLA and five collagen model molecules. From the viewpoint of energy levels, it is characteristic that the gaps of HOMO and LUMO for PLA, and (PHG, PLG, and PAG) collagen models show as 6.8, and (4.4~4.9) eV, which correspond to the organic insulators. On the other hand, the gaps of AHG and GHG collagen models give 2.2 and 2.9 eV. The gaps are considered as semiconductor-like ones. Furthermore, we pointed-out that for PLA-(AHG, GHG) bimolecular system, energy levels of unoccupied LM, LM1, LM2 for PLA model approach to the levels of occupied HM, HM1, HM2 for AHG and GHG collagen models, and then electrons on the occupied orbitals (HM, HM1, HM2) for the collagen models are able to transfer to unoccupied orbitals (LM, LM1, LM2) of PLA model in the bimolecular interaction system. In similar viewpoint, we compared the difference energy between HOMO of PLA and LUMO of PHG as 6.0 eV, while the differences between HOMO of PLA and LUMOs of (PLG, PAG) as (3.0, and 3.3) eV, respectively. Thus, electrons on occupied orbitals (HM, HM1, HM2) of the PLA model are able to transfer to unoccupied orbitals (LM, LM1, LM2) of (PLG, PAG) models better than the occupied orbitals of PLA model do the unoccupied orbitals (LM, LM1, LM2) of PHG model.
From the standpoint of intermolecular interaction energies for bimolecular systems, stabilization energies in the ranges of 30 ∼ 81 kJ/mol were shown as reasonable intermolecular interaction energies for bimolecular systems between PLA and four collagen (PAG, GHG, PHG, PLG) models, although the energy (1540 kJ/mol) of PLA-AHG(AspHypGly) collagen model is a chemical bonding one. For the PLA-AHG collagen model system, we think there may be a special bimolecular complex which has chemical bond energy. In addition, we also calculated intra- and inter-H-bond enegies for collagen I type model molecules and the bimolecular types between PLA and five collagen models by using semi-empirical MO method. The inter-H-bond enegies of the bimolecular types between PLA and four collagen models are comparable to stabilization energies of the systems by using abinitio MO calculations, and thus the nature of the intermolecular interaction can be considered to be due to the inter-H- bond (Research Data).
References
- Quirk R, Davies MC, Tendler SJB, Shakesheff KM. Surface engineering of poly (lactic acid) by entrapment of modifying species. Macromolecules. 2000;33(2):258-260. https://tinyurl.com/4rpdrf95
- Chen G, Ushida T, Tateishi T. Scaffold design for tissue engineering. Macromol Biosci. 2002;2:67-77. https://tinyurl.com/2fm4n2tv
- Castner DG, Ratner BD. Biomedical surface science: Foundations to frontiers. Surf Sci. 2000;500:28-60. https://tinyurl.com/2p8vzhz7
- Li WJ, Laurencin CT, Caterson EJ, Tuan RS, Ko FK. Electrospun nanofibrous structure: A novel scaffold for tissue engineering. J Biomed Mater Res. 2002 Jun 15;60(4):613-621. doi: 10.1002/jbm.10167. PMID: 11948520.
- Vasita R, Shanmugam I K, Katt DS. Improved biomaterials for tissue engineering applications: Surface modification of polymers. Curr Top Med Chem. 2008;8(4):341-353. doi: 10.2174/156802608783790893. PMID: 18393896.
- Rafael, Loong TL, Susan EM, Hideto T. Poly (lactic acid): Synthesis, structures, properties, processing, and applications. Polymer Science & Technology General. https://tinyurl.com/dc73aws6
- Nazre, Lin S. Theoretical Strength Comparison of Bioabsorbable (PLLA) plates and conventional stainless steel and titanium plates used in internal fracture fixation. Clinical and Laboratory Performance of Bone Plates. 1994:53-64. https://tinyurl.com/2n648fku
- Szpak Paul. Fish bone chemistry and ultrastructure: Implications for taphonomy and stable isotope analysis. J Archaeological Science. 2011;38(12):3358–3372. https://tinyurl.com/3znv5u9a
- Kramer RZ, Venugopal MG, Bella J, Mayville P, Brodsky B, Berman HM. Staggered molecular packing in crystals of a collagen-like peptide with a single charged pair. J Mol Biol. 2000 Sep 1;301(5):1191-1205. doi: 10.1006/jmbi.2000.4017. PMID: 10966815.
- Berisio R, Vitagliano L, Mazzarella L, Zagari A. Crystal structure of a collagen-like polypeptide with repeating sequence Pro-Hyp-Gly at 1.4 Å resolution: Implication for collagen hydration. Biopolymers. 2001;56:8–13. https://tinyurl.com/2udt4kn8
- Brodsky B, Ramshaw JA. The collagen triple-helix structure. Matrix Biol. 1997 Mar;15(8-9):545-54. doi: 10.1016/s0945-053x(97)90030-5. PMID: 9138287.
- Tambe N, Di J, Zhang Z, Bernacki S, El-Shafei A, King MW. Novel genipin-collagen immobilization of Polylactic Acid (PLA) fibers for use as tissue engineering scaffolds. J Biomed Mater Res B Appl Biomater. 2015 Aug;103(6):1188-1197. doi: 10.1002/jbm.b.33285. Epub 2014 Oct 11. PMID: 25308088.
- García G, Cabarcos LE, Castro RM. Study of poly (lactic-co-glycolic acid) interactions with collagen. European Polymer Journal. 2005;41:2416-2421. https://tinyurl.com/5n76sbmz
- Adamczak M, Scisłowska-Czarnecka A, Genet MJ, Dupont-Gillain CC, Pamuła E. Surface characterization, collagen adsorption and cell behaviour on poly(L-lactide-co-glycolide). Acta Bioeng Biomech. 2011;13(3):63-75. PMID: 22098254.
- Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA. Software of Quantum Chemical Calculations. 2009.
- Fukui K, Yonezawa T, Shingu H. A Molecular Orbital Theory of Reactivity in Aromatic Hydrocarbons. J Chem Phys. 1952;20:722. https://tinyurl.com/3r3eby5r
- Stewart JJP. Optimization of parameters for semiempirical methods II. Applications. J Comput Chem. 1989;10:209-220. https://tinyurl.com/356rms92
- Ohkura K, Hori H. Analysis of structure-permeability correlation of nitrophenol analogues in newborn rat abdominal skin using semiempirical molecular orbital calculation. Bioorg Med Chem. 1999 Feb;7(2):309-314. doi: 10.1016/s0968-0896(98)00200-4. PMID: 10218822.
- Vidal Bde C, Mello ML. Collagen type I amide I band infrared spectroscopy. Micron. 2011 Apr;42(3):283-289. doi: 10.1016/j.micron.2010.09.010. Epub 2010 Nov 18. PMID: 21134761.
- Darwent B. Bond Dissociation Energies in Simple Molecules. National Bureau of Standards LCCN 70602101. https://tinyurl.com/23hvmphd
- Ida T, Mizuno M, Endo K. Electronic state of small and large cavities for methane hydrate. J Comput Chem. 2002 Aug;23(11):1071-1075. doi: 10.1002/jcc.10095. PMID: 12116393.
- Ida T, Endo K, Matsumoto D, Kato N, Mizuno M, Suzuki Y, Tadokoro M. Dynamic and Static Behaviors of CH4 and CO2 in small and large cavities of hydrate. J Mol Struct. 2013;1032:275-280. https://tinyurl.com/2ckxaepf
- Endo K, Hayashi K, Ida T, Takemura T. IR and Py-GC/MS spectral simulation of polymer film by quantum chemical and quantum molecular dynamics calculations using the polymer model. Russ J Phys Chem. 2014;88(13):2370-2379.
- Lee LH. Fundamentals of adhesion. Chemical bonding and Intermolecular Forces. 1994:454.
Content Alerts
SignUp to our
Content alerts.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.