Medicine Group . 2023 June 14;4(6):1030-1038. doi: 10.37871/jbres1764.
Multivariate Statistical Process Control and Classification Applied on Prostate Cancer Screening
Øivind Riis1,2*, Andreas Stensvold3, Helge Stene-Johansen1 and Frank Westad2,4
2Department of Engineering Cybernetics, NTNU, Trondheim, Norway
3The Cancer Department, Østfold Hospital Trust, Grålum, Norway
4Idletechs AS, Trondheim, Norway
- Prostate cancer
- Multivariate analysis
- MSPC
- Classification
Abstract
Introduction: We report in this study the results of analyzing biomarkers in blood samples with two objectives; i) as an approach for screening patients by use of Multivariate Statistical Process Control (MSPC); ii) Compare various classification methods with the purpose of diagnosing prostate cancer.
Methods: We applied Principal Component Analysis (PCA) with statistical limits for outlier detection. Various splits of the data into training and test sets were chosen to evaluate the performance of classification methods as a function of the training/test sample ratio.
Results: MSPC based on 12 analytes in blood samples was shown to outperform the traditional biomarker criterion: the level of the analyte Prostate-Specific Antigen (PSA), in screening for prostate cancer. The performance of different multivariate classification techniques for classifying which of the patients in a clinical pathway for prostate cancer have malignant tumors showed that the basic method Linear Discriminant Analysis (LDA) and classification trees gave similar results, whereas adaboost gave a higher specificity but lower sensitivity.
Conclusion: The accuracy, especially the sensitivity, does not justify any clinical use of the applied classification methods with the available biomarkers. Additional medical information about the patients might enhance the accuracy with the purpose of identifying benign and malignant tumors.
Abbreviations
Introduction
The Prostate-Specific Antigen (PSA) has been used as a screening parameter for prostate cancer as a routine procedure. However, there is no general agreement on the threshold to be applied for clinical purposes, although a threshold of four is often applied. Thus, there is a need for including additional biomarkers for the inclusion of patients in the clinical pathway for prostate cancer. At the same time, it is desirable to have a better classification of which of the included patients have malignant tumors.
Tests are often based on samples from blood, serum, and urine. Many of them utilize Multivariate Data Analysis (MVDA), including classification, and techniques applied to data from different instruments for chemical and biochemical analysis. Medipally DKR, et al. [1] applied MVDA on vibrational spectroscopy of blood samples. Martynko E, et al. [2] applied MVDA on macro and trace element concentration profiles in urine determined by Inductively Coupled Plasma Optical Emission Spectroscopy (ICP-OES) and Atomic Absorption Spectroscopy (AAS). Su KY, et al. [3] used FT-IR spectroscopy for cancer screening whereas Amante E, et al. [4] used higer order methods metabolomic profiling. Lubes G, et al. [5] used MVDA on urine samples analyzed with GC-MS based metabolomics used for the identification of 27cancer volatile organic compounds as biomarkers [6]. Solovieva S, et al. [7] applied MVDA on urine samples analyzed with a potentiometric multisensor system [8,9]. To the authors' knowledge, none of them apply Multivariate Statistical Process Control (MSPC) for inclusion and surveillance of the production of health services in clinical pathways.
Within the concept of MSPC, there might be combinations of a number of variables/analytes that will indicate an out-of-control situation, whereas traditional Statistical Process Control (SPC) evaluates each variable separately. It is known that the Type 1 error increases with the number of univariate tests. Thus, the hypothesis which is the basis of this study is that applying MSPC on all variables is a better approach than screening based on PSA alone. The MSPC-based biomarker modeling approach uses blood samples that are routinely collected from the patients and hence requires no medical imaging or biopsies.
Materials and Methods
Principal Component Analysis (PCA)
PCA is a method for decomposing a matrix X into underlying latent variables or Principal Components (PCs). The criterion is to maximize the variance for the direction of each PC. Although PCA in itself is a mathematical operation, the underlying latent variables are often interpretable based on domain knowledge.
The general form of the PCA model is:
The loading vectors in P are orthonormal but not uncorrelated. The score vectors in T are orthogonal, and also uncorrelated for a model with mean-centered data. For each PC there is an associated eigenvalue that reflects the amount of variance explained by each PC. The subscript A indicates that the informative part of the data is modelled by A number of PCs, and the residuals per sample and variable (noise) are found in EA.
One of the important aspects of PCA is to separate information from noise, i.e., to find when one starts to model noise (overfitting). The optimal number of PCs might be decided upon by a number of criteria. There is, however, no single criterion that will give the optimal number of PCs for a certain application. Some criteria are i) The total sum of explained variance > a given threshold, ii) "Broken stick" and iii) Cross validated variance. Nevertheless, interpretation of explained variance, scores and loadings should always be applied when deciding on the optimal number of PCs, and preferably also by using domain specific background and experience. PCA has been investigated as an exploratory tool and for visual classification in medical applications, see e.g. Ljubicic ML, et al. [10].
PCA and Multivariate Statistical Process Control (MPSC)
Multivariate Statistical Process Control [11,12] is an extension of the classical SPC. One important aspect of SPC is that if one applies e.g. a control chart with critical limits for several individual variables, the overall significance level will decrease with the number of variables. This reduces the ability to identify outliers when the variables are correlated and if there are interactions between them.
Once a PCA model has been established on a training data set, a new sample xnew may be projected onto this model, giving the projected score for each component a:
Subscript a indicates the residual in xnew after deflating a components. The projection of a new sample is the basis for detecting out-of-control situations in MSPC.
Outlier detection
For multivariate methods such as PCA, one distinguishes between two types of outliers: i) Inside the model space, ii) In the residual space. For the first type of outliers, the Hotelling's T2 statistic is often applied. It is a multivariate generalization of the Student t-test and can be viewed as how much variance there is in one sample compared to the total variance. For more details we refer to Jackson JE [11]. In the MSPC literature the statistical limits for detecting outliers in the residual space have traditionally been based on the χ2 distribution, so-called Q-residual statistics. Again, we refer to Jackson JE [11] for details as both the Hotelling’s T2 and Q-residuals have been applied extensively in e.g. chemical process industry.
Classification methods
For an evaluation of methods for classifying patients with malignant tumors, four methods were chosen. The methods are described briefly at the conceptual level, we refer the reader to other publications for in-depth theory of the methods in the following subsections.
Linear Discriminant Analysis (LDA)
Discriminant analysis is a supervised classification method, as it is used to build a classification model for a number of pre-allocated classes [13]. This model is later used for allocating new and unknown samples to the most probable class. LDA estimates the pooled covariance of the individual classes. Some options for estimating the covariance in LDA include linear, quadratic, or a Mahalanobis-based approach.
The distance to the various classes is given by:
where x(i) is the vector of variables for each sample, is the class mean and k is an index for the class. The new sample is assigned to the class with the smallest distance from the equation above.
Support Vector Machines (SVM) classification
Support Vector Machines Classification (SVM-C) is a classification method [14] that has in general shown good performance among many classification and discrimination methods. In SVM, the data are mapped into a new feature space, and a dual representation is used with the data objects represented by their dot product. A kernel function is used to map from the original space to the feature space and can be of many forms, thus providing the ability to handle nonlinear classification cases. One useful property of SVM is that it searches for a subset of the samples that lie on the boundary between the classes. This is especially useful for inhomogeneous classes. The support vectors are the samples that were chosen for establishing the boundary.
Classification trees
Classification trees are often chosen as one of the classes of methods for comparison of performance in the case of classification/discrimination [15]. The trees are built up from the root by first selecting the variable with the best discrimination between the classes, thereafter the tree is "branched" out into a tree structure. From the first development and applications of the basic classification tree approach, several enhancements have evolved. This includes ensemble learning, boosting and bagging techniques to make the trees more robust (i.e., reduce overfitting) as well as improve the performance. In this study, the basic classification tree method is compared with the more sophisticated adaboost ensemble trees [16]. The statistics toolbox in Matlab was used for these calculations (MATLAB. version 9.6.0 (R2019a). Natick, Massachusetts: The MathWorks Inc.; 2020).
Validation of classification methods
Proper validation is one of the most important aspects of science. One way of distinguishing the concept of validation is external and internal validation [17]. The former relates to validation at the more conceptual level, such as "do I find the true signals in my system", "are the found biological markers matching theory or previous studies" or "are the results for various methods with the same purpose giving the same conclusions?", to name a few.
The internal validation is more empirical in that it tries to, in a conservative way, to train a model or models to be robust towards future known and unknown sources of variation and report suitable figures of merit. In the case of classification, this is often sensitivity or specificity or any other derived metric, depending on the application. This balance between over- and under-fitting is also called the bias-variance trade-off [18]. One way of dividing samples into training and test sets is the Kennard-Stone algorithm [19]. This algorithm finds the point in the n-dimensional space that is furthest away from the mean, then the next point is selected to be furthest away from the mean and the first point until a specified number of points has been selected. The drawback of this method is that the training set spans the whole sample space whereas the test set is confined to the region around the mean of the samples. A better option is to assign every second sample as training or test respectively, which was chosen in this study.
In addition to the Kennard-Stone algorithm, randomly selecting training and test set samples with various split ratios is common practice. This should be used with caution if there is information about sample groups that should be considered in the validation to investigate the robustness of the model, such as age groups. In the present case, random selection could be justified as the external information about the patients was scarce.
Data
Data were collected from the clinical pathway for prostate cancer at Østfold Hospital Trust during the period 2016-2017. These included blood tests, PIRADS score, Gleason score, TNM stages, diagnostic codes, and activity codes with time stamps specifying the start and end of the activities. Only the blood test was used for the work described in this article as the purpose was to search for an alternative use of PSA as a biomarker based on the blood tests routinely carried out in the pathway. Data from 238 patients (samples) were selected for analysis. The variables consisted of 12 chemical/biological blood sample analytes (Appendix 1). These biomarkers are analyzed whenever blood samples are taken routinely at hospitals or y the GP. Data for other patients were also available, however, each of these had one or more missing values. It was considered to apply imputation or directly omit the missing data in the calculations in the NIPALS algorithm for PCA. However, with the generally low correlation between the variables (see below), imputation was regarded as being not recommended for this application.
As all blood samples had been taken based on either i) PSA screening > 4.0 or ii) Palpation or other indication of enlarged prostate glands, there were no samples within the normal range for all biomarkers. The alternative was thus to simulate samples based on the normal ranges for these. An established theory when simulating data from the normal distribution is to use the range divided by four as the standard deviation, corresponding to a 95% confidence interval. The normal ranges for the biomarkers are given in table 1, they were all continuously quantitative. Simulated data were generated with the Matlab functions mvnrnd and betarnd. Inspection of the histograms for all variables revealed that they all seemed to follow a Gaussian distribution, except PSA, which empirically resembled a beta distribution. The beta distribution parameters applied were 2 and 3.
| Table 1: Overview of basic statistics of the variables. See appendix A for full variable names. | |||||||
| Variable | Mean | Min | Max | Range | Std Dev | Mean | Mean Dimulated |
| HB | 15 | 13.5 | 16.5 | 3 | 0.75 | 15.1 | 15 |
| LEUK | 7.25 | 3.5 | 11 | 7.5 | 1.875 | 7.2 | 7.2 |
| PSA | 3.75 | 0 | 6.5 | 6.5 | 1.63 | 8.69 | 3.75 |
| SAFOS | 70 | 35 | 105 | 70 | 17.5 | 73.3 | 69.5 |
| SALAT | 40 | 10 | 70 | 60 | 15 | 31 | 39.9 |
| SASAT | 30 | 15 | 45 | 30 | 7.5 | 27.8 | 29.8 |
| SHDLK | 1.45 | 0.8 | 2.1 | 1.3 | 0.325 | 1.28 | 1.47 |
| SK | 4.3 | 3.6 | 5 | 1.4 | 0.375 | 4.37 | 4.3 |
| SKOL | 5.85 | 3.9 | 7.8 | 3.9 | 0.975 | 4.92 | 5.68 |
| SKREAT | 82.5 | 60 | 105 | 45 | 11.25 | 84.5 | 82.4 |
| SNA | 141 | 137 | 145 | 11.3 | 2.5 | 141.5 | 141.1 |
| TRC | 300 | 150 | 400 | 300 | 72.5 | 219 | 300.3 |
Results and Discussion
The analysis of the data served two purposes. The first was to show how MSPC can be applied in a diagnostic setting, based on all the blood sample biomarkers. The second was to investigate the predictability of the patient’s medical status from these biomarkers.
An initial PCA was performed on the 228 samples. By inspection of plots of raw data as well as interpretation of scores and loading, it was revealed that some of the samples had extreme values for one or more analytes. The optimal dimensionality of the model was found keeping these in the model will mean that only a few of the samples will span many of the underlying dimensions, which can give a skewed representation of the model space. 11 samples were lying outside of the critical limit at the 0.1% level for one or both of the two criteria for outlier detection as described above. Although we are not, in general, advocating for removing samples blindly as outliers just because they lie outside a critical limit, we find this to be justified in this case.
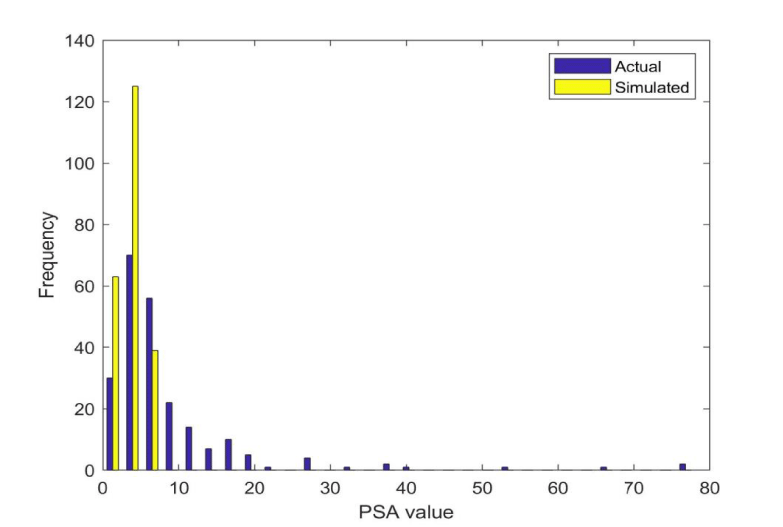
As the main biomarker for screening prostate cancer is PSA, histograms for this analyte are shown for the actual and simulated data in figure 1. 106 samples in the simulated data were found to be lying outside of the threshold of 4.0, thus, PSA in itself cannot distinguish sufficiently well between simulated and actual samples. The actual data may have some inherent correlations based on underlying biological factors. Therefore, a correlation table based on the empirical data was generated for the 227 remaining samples. Interestingly enough, only the correlation between SALAT and SASAT was higher than 0.3, which means that these univariate biomarkers each represent something unique in the blood. 227 random samples were generated.
Using PCA for Multivariate Process Control (MSPC)
The procedure for establishing an MSPC model and the results from projecting other samples onto this model are described below.
Establishing the model for MSPC: The first step in the analysis was to establish a PCA model for the 227 remaining samples. As the variables had very different units and ranges of variation, they were first centered and scaled to unit variance.
From the analysis and interpretation of the explained variance and the loadings, the optimal number of components was assessed to be 11. This accounted for 97.6% of the variance. This is in agreement with the univariate correlations and an interesting finding, as in most biological systems there will be redundancy, thus the underlying model rank is usually significantly lower than the number of variables. However, for these biomarkers, it seems that they span more or less their own underlying dimension. A model was then calculated for 60% of the simulated data, setting the optimal dimensionality to 11 for the subsequent projection of the actual data and the simulated test set. The reason for setting aside 40% of the samples was to test if the simulated data would be classified as being outside of the model. Only projecting the actual patient data onto a model on all simulated samples would not be a proper procedure. The Kennard-Stone sample selection method [19] was applied to divide the samples into training and test sets.
Projecting the actual samples onto the model
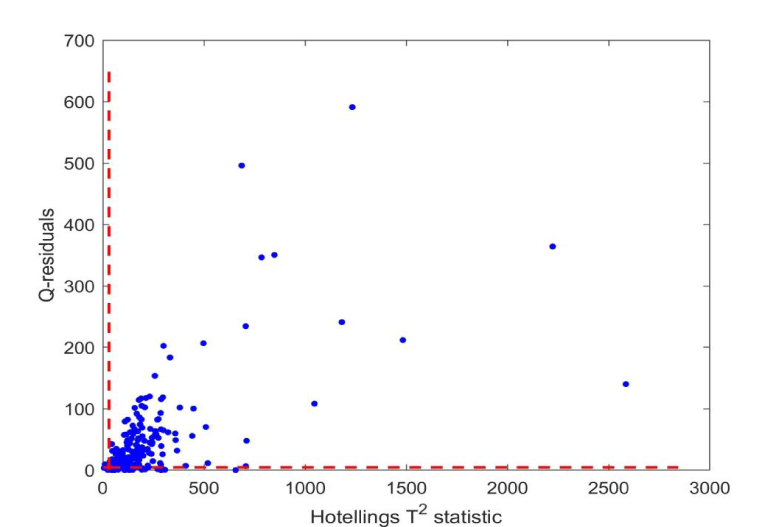
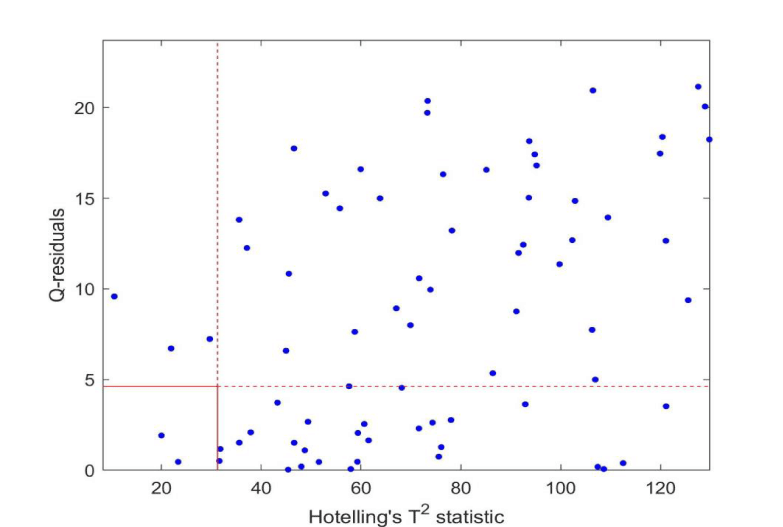
The 227 samples were projected onto the model by estimating the scores from the centered and scaled data and the loadings. The critical limits from Hotelling's T2 and Q-residuals were applied to identify samples outside the model as well as the residual space. Figures 2,3 (zoomed in) show the samples in a combined plot for identifying outliers. The confidence level was 99.5%. As can be seen, all samples except three fall outside one or more of the limits, thus all patients are classified as having a deviating pattern for the biomarkers based on a projection onto the multivariate model. When projecting the 40% simulated samples onto this model, only three samples were outside of the Q-residual limit.
A common threshold for PSA for further consultation by medical doctors regarding prostate cancer is 4.0. In this case, this left 61 patients below the threshold. These patients were enrolled in the clinical patient pathway due to other tests, e.g. palpation and biopsy of the prostate and by Magnetic Resonance Imaging (MRI), and they should all show abnormal serum levels for one or more biomarkers. However, if one looked at a specific biomarker, the samples lying outside the 99.5% confidence interval would lie inside the limits for other biomarkers. Only a multivariate approach can identify the actual patients as outliers compared to the simulated data.
Classification of patients with malignant tumors from the blood biomarker variables
The 227 samples, after omitting the outliers, were first divided into training and test sets. A binary column, often named one-hot encoding, representing the diagnostic outcome of the medical doctor's evaluation, defined the categorical variable for classification, with malignant tumor as one class and all other diagnostic outcomes as "non-tumor". The reason for this binary classification scheme was that the "non-tumor" class represented many other diagnostic stages, the most prominent was "other abnormal serum concentration" which could pertain to any of the individual biomarkers. 52 samples were categorized as malignant.
For evaluation of the results from classification, the so-called duplex version of the Kennard-Stone was applied, assigning every second sample to the training and test set respectively, giving a 50/50 split of training and test. In addition, 100 random realizations of 50/50, 60/40, 70/30, and 80/20 splits of training and test were simulated. The adaboost classification was run with 100 learning cycles.
The results from the various classification methods are presented in tables 2-4. All the results from the random splits are based on 100 realizations. They show that the classification metrics of the tumor diagnosis, set at the stage named "investigation in the clinical pathway for prostate cancer", are not good enough for implementation as a clinical procedure.
| Table 2: Results for LDA for the various splits of training and test sets. | |||||
| Training | Duplex | 50/50 | 60/40 | 70/30 | 80/20 |
| Sensitivity | 0.92 | 0.89 | 0.84 | 0.80 | 0.80 |
| Specificity | 0.84 | 0.83 | 0.79 | 0.77 | 0.75 |
| Test | Duplex | 50/50 | 60/40 | 70/30 | 80/20 |
| Sensitivity | 0.25 | 0.26 | 0.34 | 0.33 | 0.34 |
| Specificity | 0.76 | 0.77 | 0.72 | 0.70 | 0.68 |
| Table 3: Results for adaboost for the various splits of training and test sets. | |||||
| Training | Duplex | 50/50 | 60/40 | 70/30 | 80/20 |
| Sensitivity | 0.83 | 0.81 | 0.6 | 0.45 | 0.32 |
| Specificity | 1.00 | 0.99 | 0.99 | 0.98 | 0.98 |
| Test | Duplex | 50/50 | 60/40 | 70/30 | 80/20 |
| Sensitivity | 0.07 | 0.12 | 0.11 | 0.08 | 0.07 |
| Specificity | 0.87 | 0.84 | 0.85 | 0.87 | 0.89 |
| Table 4: Results for classification trees for the various splits of training and test sets. | |||||
| Training | Duplex | 50/50 | 60/40 | 70/30 | 80/20 |
| Sensitivity | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Specificity | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Test | Duplex | 50/50 | 60/40 | 70/30 | 80/20 |
| Sensitivity | 0.29 | 0.27 | 0.28 | 0.3 | 0.28 |
| Specificity | 0.65 | 0.76 | 0.74 | 0.76 | 0.75 |
There are many reasons for the poor performance on the test set compared to the training set. Firstly, the blood test does not relate directly to the patient's state w.r.t to cancer. Secondly, the patients not diagnosed with cancer are themselves quite heterogeneous w.r.t. their medical condition. The ideal situation in the case of classification is to have a homogeneous class of "normal" patients whereas the "abnormal" deviate for one reason or another. Finally, the tumors are not a homogeneous class in themselves.
Apart from evaluating the classification results as such in terms of specificity and sensitivity, a comparison of the various methods with the purpose of evaluating if they give the same results, is an important aspect. LDA is often regarded as a benchmark for comparison with more sophisticated methods. In this case, there is a worse performance on the test set compared to the training set for all methods. The results for LDA and the basic classification tree method show similar performance on the test set.
Adaboost gives 10% better performance on the specificity, but a much worse performance on the sensitivity. In most medical applications, as is also the case in this study, high sensitivity is preferable to high specificity: patients with severe conditions are being treated at an early stage.
The SVM classification gave 0% sensitivity for both the training and test set (not shown). The specificity was 100% for training as well as for the test set. The settings of hyper-parameters were chosen based on a grid search with 20 segment random cross-validation to avoid overfitting. Only 53 of the samples were selected as support vectors in the SVM, of which 29 were benign and 24 were malignant. None of the kernel options gave different results.
Another approach to modelling is to calculate ratios of variables as input to the model. As an additional procedure, PSA was divided onto the other biomarkers to produce a derived data table. The results from LDA on these data are given in table 5. Sensitivity has improved by around 15% at the cost of decreased specificity in similar numbers. This might be a preferred modelling option in a clinical setting.
| Table 5: Results for LDA for the various splits of training and test sets on the ratio derived data. | |||||
| Training | Duplex | 50/50 | 60/40 | 70/30 | 80/20 |
| Sensitivity | 0.96 | 0.91 | 0.90 | 0.91 | 0.89 |
| Specificity | 0.63 | 0.62 | 0.54 | 0.48 | 0.43 |
| Test | Duplex | 50/50 | 60/40 | 70/30 | 80/20 |
| Sensitivity | 0.39 | 0.41 | 0.53 | 0.56 | 0.61 |
| Specificity | 0.63 | 0.61 | 0.51 | 0.45 | 0.41 |
As an additional analysis in light of the above findings, A PCA model on the 227 samples revealed that there was no clear separation of the classes, thereby confirming that there was no systematic variation in the data pertaining to the classes when an unsupervised method such as PCA was applied. This is an indication of why the supervised classification methods do not perform well on this data set.
A closer investigation into the data regarding classification accuracy pertaining to the age groups of the patients would be of interest, unfortunately, age was not part of the dataset due to limited access for exporting variables/information from the software/database where the information was stored. According to Putra IB, et al. [20], there is only a week correlation between PSA and age, therefore one cannot assume that age as an additional variable would change the results significantly.
Conclusion
The methodology presented in this study investigates the potential for screening patients for inclusion in the clinical pathway for prostate cancer and also predicting the occurrence of malign tumors, which is in line with the concepts of Precision Medicine (PM) utilizing multivariate statistics. MSPC is extensively used in many industrial applications, however to the best of our knowledge rarely used in the provisioning of health services. The results showed that the multivariate approach was far more effective in detecting the deviating pattern of the biomarkers compared to the single PSA criterion.
The summary from the classification models gave quite different results for the various methods. LDA and classification trees gave similar performance on the test set for the specificity for the random splits of training and test sets, although the classification tree method over-fitted the training set. For the double Kennard-Stone approach, the specificity was higher for LDA. It is also worth noticing that the sensitivity for the training set for the adaboost method was reduced with a higher training/test set split ratio. The results for SVM were surprising, as SVM normally ranks among the best methods in general, as reported in the literature. The fact that only 53 samples were selected as support vectors in the model, and thus does not indicate overfitting, further adds to this being an unexpected result.
As the number of digitized measurements related to a person's health is increasing rapidly there will be ample opportunities for the use of MSPC as a software-based biomarker approach.
Acknowledgments
Institutional review board statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Ethics Committee, Rek Sor-Ost protocol code 2017/20) 20 Jan 2017.
Informed consent statement
Patient consent was waived due to general consent for including patients from Ethics Committee, Rek Sor-Ost (protocol code 2016 Bredt samtykke kreft - felles (3)) 16.07.2018 for Ostfold Hospital Trust regarding quality assurance activities/projects by the cancer department
Conflicts of interest
Frank Westad represents the company Idletechs who was hired as a consultant in machine learning. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Funding
This research was funded by South-Eastern Norway Regional Health Authority grant 306 number 16/00528-24.
References
- Medipally DKR, Cullen D, Untereiner V, Sockalingum GD, Maguire A, Nguyen TNQ, Bryant J, Noone E, Bradshaw S, Finn M, Dunne M, Shannon AM, Armstrong J, Meade AD, Lyng FM. Vibrational spectroscopy of liquid biopsies for prostate cancer diagnosis. Ther Adv Med Oncol. 2020 Jul 30;12:1758835920918499. doi: 10.1177/1758835920918499. PMID: 32821294; PMCID: PMC7412923.
- Martynko E, Oleneva E, Andreev E, Savinov S, Solovieva S, Protoshchak V, Karpushchenko E, Sleptsov A, Panchuk V, Legin A, Kirsanov D. Non-invasive prostate cancer screening using chemometric processing of macro and trace element concentration profiles in urine. Microchemical Journal. 2020;159:105464. doi: 10.1016/j.microc.2020.105464.
- Su KY, Lee WL. Fourier Transform Infrared Spectroscopy as a Cancer Screening and Diagnostic Tool: A Review and Prospects. Cancers (Basel). 2020 Jan 1;12(1):115. doi: 10.3390/cancers12010115. PMID: 31906324; PMCID: PMC7017192.
- Amante E, Salomone A, Alladio E, Vincenti M, Porpiglia F, Bro R. Untargeted Metabolomic Profile for the Detection of Prostate Carcinoma-Preliminary Results from PARAFAC2 and PLS-DA Models. Molecules. 2019 Aug 22;24(17):3063. doi: 10.3390/molecules24173063. PMID: 31443574; PMCID: PMC6749415.
- Lubes G, Goodarzi M. GC-MS based metabolomics used for the identification of cancer volatile organic compounds as biomarkers. J Pharm Biomed Anal. 2018 Jan 5;147:313-322. doi: 10.1016/j.jpba.2017.07.013. Epub 2017 Jul 17. PMID: 28750734.
- Guo J, Zhang X, Xia T, Johnson H, Feng X, Simoulis A, Wu AHB, Li F, Tan W, Johnson A, Dizeyi N, Abrahamsson PA, Kenner L, Xiao K, Zhang H, Chen L, Zou C, Persson JL. Non-invasive Urine Test for Molecular Classification of Clinical Significance in Newly Diagnosed Prostate Cancer Patients. Front Med (Lausanne). 2021 Sep 14;8:721554. doi: 10.3389/fmed.2021.721554. PMID: 34595190; PMCID: PMC8476767.
- Solovieva S, Karnaukh M, Panchuk V, Andreev E, Kartsova L, Bessonova E, Legin A, Wang P, Wan H, Jahatspanian I, Kirsanov D. Potentiometric multisensor system as a possible simple tool for non-invasive prostate cancer diagnostics through urine analysis. Sensors and Actuators B: Chemical. 2019;289:42-47. doi: 10.1016/j.snb.2019.03.072.
- Aggio RB, de Lacy Costello B, White P, Khalid T, Ratcliffe NM, Persad R, Probert CS. The use of a gas chromatography-sensor system combined with advanced statistical methods, towards the diagnosis of urological malignancies. J Breath Res. 2016 Feb 11;10(1):017106. doi: 10.1088/1752-7155/10/1/017106. PMID: 26865331; PMCID: PMC4876927.
- Vergel ÁJS, Mendoza LE, Delgado BM. Analysis of energy and major components in chromatographic signals for the diagnosis of prostate cancer. Respuestas. 2019;24:76-85.
- Ljubicic ML, Madsen A, Juul A, Almstrup K, Johannsen TH. The Application of Principal Component Analysis on Clinical and Biochemical Parameters Exemplified in Children With Congenital Adrenal Hyperplasia. Front Endocrinol (Lausanne). 2021 Aug 31;12:652888. doi: 10.3389/fendo.2021.652888. PMID: 34531821; PMCID: PMC8438425.
- Jackson JE. A user’s guide to principal components. John Wiley & Sons; 2005.
- Ge Z, Song Z. Multivariate statistical process control: Process monitoring methods and applications. Springer Science & Business Media; 2012.
- Solberg HE. Editorial: Discriminant analysis in clinical chemistry. Scand J Clin Lab Invest. 1975 Dec;35(8):705-12. doi: 10.3109/00365517509095801. PMID: 1108173.
- Corte C, Vapnik V. Support vector machines. Machine Learning. 1995;20:273-297. doi: 10.1007/bf00994018.
- Breiman L, Friedman JH, Olshen RA, Stone CJ. Classification and Regression Trees. Routledge; 2017.
- Schapire RE. Explaining adaboost. In: Empirical Inference. Springer; 2013. p.37-52.
- Westad F, Marini F. Validation of chemometric models - a tutorial. Anal Chim Acta. 2015 Sep 17;893:14-24. doi: 10.1016/j.aca.2015.06.056. Epub 2015 Aug 10. PMID: 26398418.
- Brain D, Webb GI. The need for low bias algorithms in classification learning from large data sets. In Proceedings of the European Conference on Principles of Data Mining and Knowledge Discovery. Springer; 2002. p.62-73.
- Kennard RW, Stone LA. Computer aided design of experiments. Technometrics. 1969;11:137-148. doi: 10.2307/1266770
- Putra IB, Hamid AR, Mochtar CA, Umbas R. Relationship of age, prostate-specific antigen, and prostate volume in Indonesian men with benign prostatic hyperplasia. Prostate Int. 2016 Jun;4(2):43-8. doi: 10.1016/j.prnil.2016.03.002. Epub 2016 Mar 11. PMID: 27358842; PMCID: PMC4916066.
Content Alerts
SignUp to our
Content alerts.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.