New Insights to Understand the CoMFA Analysis within the Density Functional Theory Framework

The Three-Dimensional Quantitative Structure-Activity Relationship (3D QSAR) models now have a wide range of applications; however, new methodologies are required due to the complexity in understanding their results. This research presents a generalized version of quantum similarity field and chemical reactivity descriptors within the density functional theory framework.

By taking reference compounds, this generalized methodology can be used to understand the biological activity of a molecular set. In this sense, this methodology allows to study of the CoMFA in quantum similarity and chemical reactivity. It is feasible to investigate steric and electrostatic effects on local substitutions using this method. They were considering that how these methodologies could be used when the receptor is known or unknown.

Our research group demonstrated that the Comparative Molecular Field Analysis (CoMFA) and the Comparative Molecular Similarity Indexes Analysis (CoMSIA) could be interpreted in terms of Molecular Quantum Similarity (MQS) and Density Functional Theory (DFT)-based reactivity descriptors in two recent articles [1].

Since the CoMFA and CoMSIA analyses have numerous applications in Three-Dimensional Quantitative Structure-Activity Relationships (3D QSAR) studies, additional considerations about these approaches in the DFT context are provided in this research.

The MQS proposed by Carbó and co-workers within the DFT approach is a significantly applicable field [2-6]. The density function is an essential variable in the MQS field [7-11]; thus, it is plausible to assume that it can be linked to chemical reactivity descriptors such as chemical hardness (ɳ), softness (S), electrophilicity (ω), and Fukui Functions.

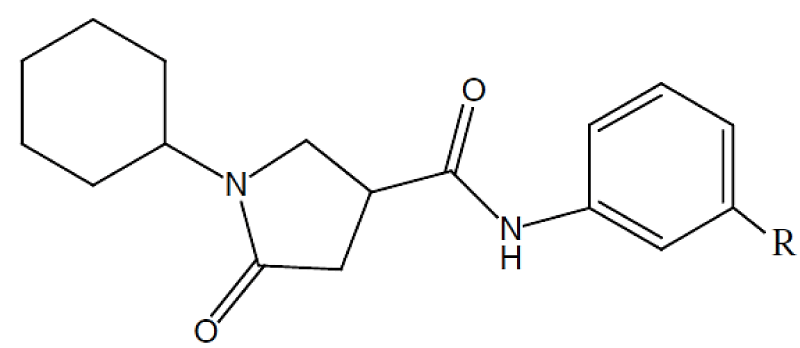
Utilizing a series of pyrrolidine carboxamides studied by Kumar and Siddiqi [12], we intend to demonstrate new insight on the comprehension of the CoMFA results within the DFT context using this hybrid methodology (connecting the MQS and chemical reactivity). With cross-validated and conventional correlation values of 0.626 and 0.953, they reported a statistically significant CoMFA analysis. As a result, the main goal is to understand this correlation between the MQS field and chemical reactivity descriptors and to demonstrate novel connections between these two methodologies that can be applied to the CoMFA analysis.

Quantum Object Sets (QOS)

Considering the following set: $Z=\left\{z_I|I=1,N\right\}$ , where N is the Cartesian product of two sets: $Z=\left\{P\times M\right\}$ is the set of the objects, and $M=\left\{m_I|I=1,N\right\}$ is the set of tags. Therefore we can write: $\forall I=1,{\text{ N:z}}_I=\left(p_I;m_I\right)\in Z$ [2,13]. In this sense, a (QOS) is a tagged set: $Q=P\times S$ consisting of a group of submicroscopic objects and a set of quantum mechanical Density Function (DF): $S=\left\{{\rho }_I|I=1,N\right\}$ as elements of the tag set.

We can define a central averaged DF of this type using the Hilbert semi space tag set S and the expression:

${\rho }_C=N^{-1}{\displaystyle \sum _I{\rho }_I\to \langle {\rho }_C\rangle =N^{-1}{\displaystyle \sum _I\langle {\rho }_I\rangle }}=N^{-1}{\displaystyle \sum _I{\upsilon }_I}={\upsilon }_C\text{ (1)}$

The DF Minkowski norms are defined as follows:

$\forall I=1,N:\langle {\rho }_I\rangle ={\displaystyle \underset{D}{\int }{\rho }_I(r)dr={\upsilon }_I}\text{ (2)}$

Therefore, the centroid DF can describe the arithmetic average of all involved quantum objects' particles. We define tag set H associated with the DF set S to relate the shape functions associated with the quantum set, resulting in:

$\begin{array}{l}S=\left\{{\rho }_I|I=1,N\right\}\to \forall \langle {\rho }_I\rangle ={\upsilon }_I\wedge {\sigma }_I=\\ {\upsilon }_I^{-1}{\rho }_I\wedge \langle {\sigma }_I\rangle =1\to H=\left\{{\sigma }_I|I=1,N\right\}\text{ (3)}\end{array}$

The shape centroid function can be written as follows using equation 3:

$\begin{array}{l}{\sigma }_C=N^{-1}{\displaystyle \sum _I{\sigma }_I}\to \langle {\sigma }_C\rangle =\\ N^{-1}{\displaystyle \sum _I\langle {\sigma }_I\rangle }=N^{-1}N=1\text{ (4)}\end{array}$

Local molecular quantum similarity measure: A generalized version

Intending to obtain a generalized Hirshfeld approach to our systems, we considered the electron density ρ(r) in contribution ρ x1 (r), where x is an atom [4,14-18]. These contributions enable the definition of an atom in a reference system and the investigation of its (dis)similarity on a molecular set (i.e., substituent effect analysis) [19].

$Z_{A,B}^{Local,x}=\frac{Z_{AB}}{\sqrt{Z_{AA}{Z}_{BB}}}=\frac{{\displaystyle \iint w_{x,AB}{\rho }_A(r){\rho }_B(r)d{r}_{A}d{r}_B}}{\sqrt{{\left({\displaystyle \int w_{x,A}(r){\rho }_A(r)d{r}_A}\right)}^2{\left({\displaystyle \int w_{x,B}(r){\rho }_B(r)d{r}_B}\right)}^2}}\text{ (5)}$

We can represent the global Carbó index as local contributions as equation 5 is a generalized Hirshfeld approach to our systems, where x is given as an atom [1]. It is possible to investigate the local similarity and substituent effects on some reference compounds in this context (QOS).

Reactivity descriptors

The CoMFA analysis is based on physical-chemistry properties related to electrostatic and steric effects. In this way, global chemical descriptors like chemical potential, hardness, and electrophilicity index, as well as local reactivity descriptors such as the Fukui Functions, can be linked to these properties [1]. Global reactivity indices provide information on a chemical system's reactivity or stability in the face of external disturbances in the DFT context.

The chemical potential (μ) is defined as the tendency of electrons to leave the electron cloud and is calculated using the following equation:

$\mu \approx \frac{{\epsilon }_H+{\epsilon }_L}{2}\text{ (6)}$

where (εH) and (εL) are the energy of the (HOMO) and (LUMO), respectively [20,21]. According to Pearson et al. investigation [22], chemical hardness is defined using equation 14.

$\eta \approx {\epsilon }_L-{\epsilon }_H\text{ (7)}$

From equation (7), we obtain the softness [23] as:

$S=\frac{1}{\eta }\text{ (8)}$

Finally, the electrophilicity index (ω) [24,25] is defined using equations 6 and 7. This index is defined as a measure of the system's stabilization energy when electrons saturate it from the external environment, and it is calculated as follows:

$\omega =\frac{{\mu }^2}{2\eta }\text{ (9)}$

Finally, the Fukui Functions (equations 10 and 11) are defined as the derivative of the electronic density with respect to the number of electrons when the external potential is kept constant:

$f_k^{+}\approx {\displaystyle \underset{k}{\int }\left[{\rho }_{N+1}\left(\overrightarrow{r}\right)-{\rho }_N\left(\overrightarrow{r}\right)\right]}=\left[q_k\left(N+1\right)-q_k\left(N\right)\right]\text{ (10)}$

$f_k^{-}\approx {\displaystyle \underset{k}{\int }\left[{\rho }_N\left(\overrightarrow{r}\right)-{\rho }_{N-1}\left(\overrightarrow{r}\right)\right]}=\left[q_k\left(N\right)-q_k\left(N-1\right)\right]\text{ (11)}$

The electron population at the kth atomic site in a molecule is defined by qk. ( $f_k^{+}$ ) and ( $f_k^{-}$ ) are governing the susceptibility for the nucleophilic and electrophilic attack, respectively [26-29].

Quantum operators to calculate local similarity

The Dirac delta distribution $\Omega (r_1,r_2)=\delta (r_1,r_2)$ [30], also known as the overlap molecular quantum similarity measure, is one of the most commonly used operators in quantum similarity measure and related the volume associated with the overlap of the two densities ρA (r) and ρB (r):

$\begin{array}{l}{Z}_{A,B}^{Local,x}(\Omega )=\frac{Z_{AB}(\Omega )}{\sqrt{Z_{AA}(\Omega )Z_{BB}(\Omega )}}\\ =\frac{{\displaystyle \iint w_{x,AB}{\rho }_A(r)\delta (r_1-r_2){\rho }_B(r)d{r}_{A}d{r}_B}}{\sqrt{{\left({\displaystyle \int w_{x,A}(r){\rho }_A(r)d{r}_A}\right)}^2{\left({\displaystyle \int w_{x,B}(r){\rho }_B(r)d{r}_B}\right)}^2}}\\ =\frac{{\displaystyle \iint w_{x,AB}{\rho }_A(r){\rho }_B(r)d{r}_{A}d{r}_B}}{\sqrt{{\left({\displaystyle \int w_{x,A}(r){\rho }_A(r)d{r}_A}\right)}^2{\left({\displaystyle \int w_{x,B}(r){\rho }_B(r)d{r}_B}\right)}^2}}\text{ (12)}\end{array}$

It is possible to collect information about the electron concentration in the molecule using equation 12, which also indicates the degree of overlap between the compared compounds.

The Coulomb operator $\Phi (r_1,r_2)$ , defined as $\Phi (r_1,r_2)=|r_1-{r_2|}^{-1}$ is another widely used operator in quantum chemistry. It represents the electronic Coulomb repulsion energy between molecular densities ρA(r) and ρB(r) is written as:

$\begin{array}{l}{Z}_{A,B}^{Local,x}(\Phi )=\frac{Z_{AB}(\Phi )}{\sqrt{Z_{AA}(\Phi )Z_{BB}(\Phi )}}\\ =\frac{{\displaystyle \iint w_{x,AB}{\rho }_A(r)\left(1/|r_1-r_2|\right){\rho }_B(r)d{r}_{A}d{r}_B}}{\sqrt{{\left({\displaystyle \int w_{x,A}(r){\rho }_A(r)d{r}_A}\right)}^2{\left({\displaystyle \int w_{x,B}(r){\rho }_B(r)d{r}_B}\right)}^2}}\\ =\frac{{\displaystyle \iint w_{x,AB}{\rho }_A(r){\rho }_B(r)d{r}_{A}d{r}_B}}{\sqrt{{\left({\displaystyle \int w_{x,A}(r){\rho }_A(r)d{r}_A}\right)}^2{\left({\displaystyle \int w_{x,B}(r){\rho }_B(r)d{r}_B}\right)}^2}}\text{ (13)}\end{array}$

According to the Schwartz integral, the Carbó index is limited to the range (0,1), where C_AB = 0 indicates dis(similarity) and C_AB = 1 indicates self-similarity.

${\left[{\displaystyle \int {\rho }_A(r){\rho }_B(r)dr}\right]}^2\le {\displaystyle \int {\rho }_A^2(r)dr}{\displaystyle \int {\rho }_B^2(r)dr}\text{ (14)}$

Quantum similarity matrix

The quantum similarity Matrix can be related to a [N × N] metric associated with a (QOS) tag set formed of quantum mechanical density function $S=\left\{{\rho }_I|I=1,N\right\}$ as:

$Z=\left[\begin{array}{c}\langle z_1|\\ \langle z_2|\\ ⋮\\ \langle z_N|\end{array}\right]=\left[\langle z_1|\langle z_2|\cdots \langle z_N|\right]\text{ (15)}$

Rows and columns are equivalent in equation 15. In this regard, we have the following:

$\begin{array}{l}Z=\left\{Z_{IJ}=\langle {\rho }_I|{\rho }_J\rangle |I,J=1,N\right\}\\ \wedge |z_I\rangle =\left\{Z_{JI}|J=1,N\right\}\\ \wedge \langle z_I|=\left\{Z_{IJ}|J=1,N\right\}\text{ (16)}\end{array}$

The symmetry of the matrix Z is another significant property, according to:

$Z=Z^T\to \forall I,J:Z_{IJ}=Z_{JI}\text{ (17)}$

Considering these properties associated with the similarity matrix, we can express the local molecular similarity measures using the overlap and coulomb operators (equations 12 and 13).

Joining QS and chemical reactivity

It is conceivable to consider a set of specified vectors and assign a center to this QOS, according to Carbó, et al. [31] investigation. Therefore, Fukui Functions can be used to represent a QOS as follows:

$M=\left\{|I\rangle I=1,N\right\}\text{ (18)}$

The first order densities in equation 23 can be constructed using a set of Molecular Orbital (MO) of shape function contributions as follows:

$P=\left\{{\sigma }_I=|I\rangle \langle I|I=1,N\right\}\text{ (19)}$

P elements represent the squared MO modules. Using these considerations, we can relate the frontier orbital (HOMO and LUMO) to the QOS. We can construct a linear combination of P to the first-order density functional by defining {w1} as the number of occupations in the MOs as follows [32]:

$\rho ={\displaystyle \sum _I{w}_I{\sigma }_I}\text{ (20)}$

where (i) ν is the number of electrons: ${\displaystyle \sum _I{w}_I}=\nu$ . (ii) Where the Minkowski norms of the elements of the shape function set P are normalized to unity, belonging to the MO set normalization $\left(\forall I:\langle {\sigma }_I\rangle =1\right)$ .

Therefore we can use an average function to define a centroid shape function

${\sigma }_C=N^{-1}{\displaystyle \sum _I{\sigma }_I}\to \langle {\sigma }_C\rangle =1\text{ (21)}$

Each element of set P can be compared to the centroid function in this way and can be constructed as:

$\forall I:{\theta }_I={\sigma }_I-{\sigma }_C\to Z=\left\{{\theta }_I|I=1,N\right\}\text{ (22)}$

Finally, the Minkowski pseudonorm of the centroid shape function set Z can be written as:

$\forall I:{\theta }_I=\langle {\sigma }_I-{\sigma }_C\rangle =\langle {\sigma }_I\rangle -\langle {\sigma }_C\rangle =0\text{ (23)}$

Therefore the shifted elements have a null Minkowski pseudonorm, where the shape function is comprised of N linearly independent elements. Using these relations, we can make quantum similarity utilizing the Fukui Functions on the QOS, taking into account a reference compound.

$Z_{AB}(f^{+/-}(r))=\frac{{\left[f^{+/-}(r)\right]}_A{\left[f^{+/-}(r)\right]}_B}{\sqrt{{\left[f^{+/-}(r)\right]}_A^2{\left[f^{+/-}(r)\right]}_B^2}}\text{ (24)}$

Scales of convergence quantitative [1] can construct using equation 24, as long as this equation depicts a possible connection between quantum similarity and chemical reactivity. It can also be used to determine quantum similarity based on local chemical reactivity (Fukui functions). The contour maps generated by the CoMFA and CoMSIA results can be related to these measures. In addition to what is provided by the 3D-QSAR studies, the other advantage of the proposed methodology is demonstrating a possible way to quantify the biological activity of the compounds.

Table 1 contains the given molecular set, and All the compounds were optimized using B3LYP exchange-correlation functional [33(a,b)] at 6w-31G(d,p) level of theory, and gaussian 09 was used to perform all of the optimizations [34].

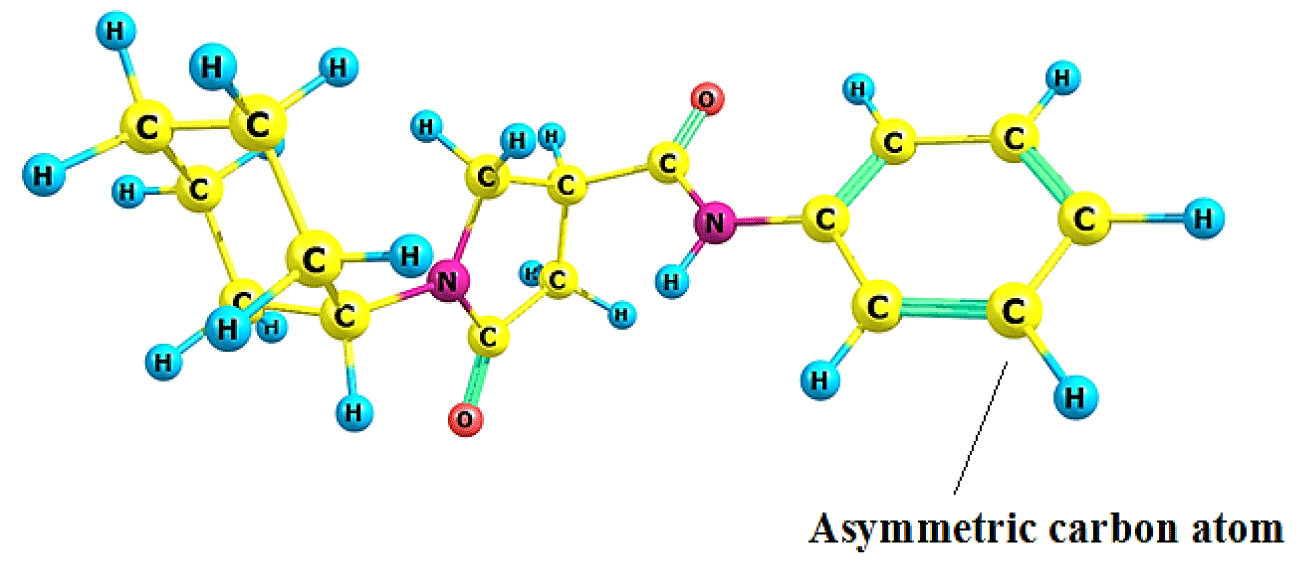
The Topo-Geometrical Superposition Algorithm (TGSA) [35,36] was utilized for the alignment that tries to overlap as many structural elements as possible. Chemical bonds and sequences of two chemical bonds are represented by these structural elements, which always involve the same type of atoms in the molecules being compared. The structure selected (compound 1) for the superimposition process is shown in figure 1.

Figure 1: The structure selected (compound 1) for the superimposition process.

Table 1 displays the Carbó values using equation 12, which is frequently associated with the steric effect, representing a possible form to quantify the steric map reported by the CoMFA data.

The compound with the highest local similarity regard to compound 1 (reference compound) is compound 2 with a value of 0.985 and an euclidean distance of 0.721; the compound with the lowest similarity is compound 5, with a value of 0.672 and an euclidean distance of 3.899 (Table 2). In the halogen group, these results indicate the lowest steric effects. However, the higher steric effects are on the group (methyl trifluoride, compound 5) with more size, but not on the group isopropyl, compound 7 with less size. The similarity between compounds 5 and 7 is 0.739 with a euclidean distance of 3.539; this similarity value is consistent with their respective pIC₅₀ values of 5.312 and 5.226.

The Coulomb values are shown in table 3 using the Coulomb operator (equation 13), which is associated with electrostatic effects and can be linked to the electrostatic map in the CoMFA analysis.

Table 4 shows that compound 3 has a higher electronic similarity concerning the reference compound 1 with 0.998 and a euclidean distance of 4.114 (Table 5). Compound 3 has a substituent chlorine which has an inductive effect. On the other hand, compound 5 has the lowest electronic similarity with 0.925 and a euclidean distance of 19.924 since compound 5 has the group methyl trifluoride and therefore presents a significant inductive effect. The chemical descriptor supported on DFT is used to analyze the electrostatic effects. The global reactivity indexes are shown in table 6.

The chemical potential (μ = -3.198 eV), Hardness (ɳ = 5.529 eV), softness (S = 0.181), and electrophilicity ω = 0.965 eV of reference compound 1 are shown in tables 6,7 and these values are matched to an experimental pIC₅₀ (4.972). This reference compound has greater hardness values (ɳ = 5.529 eV), while compound 6 has the lowest hardness (ɳ = 4.529 eV) with a softness value of (S = 0.221 eV^-1) and simultaneously it has higher electrophilicity (ω = 2.156 eV). This finding can be explained by the presence of the nitro group, which is an electron-withdrawing group. Chemical potential (μ = -3.498 eV), hardness (ɳ = 5.478 eV), softness (S = 0.183 eV^-1) and an electrophilicity (ω = 1.117 eV) are all in compound 2 with the highest experimental activity (pIC₅₀ = 6.05). These global descriptors suggest a local analysis, and the Fukui Function on the asymmetric carbon atom is employed to build this local study (Figure 1).

This research reports new insights on the generalized relationship between quantum similarity and chemical reactivity. This hybrid methodology allows us to investigate steric and electrostatic effects in quantitative scales of convergence and substituent effects, among others. In this way, the CoMFA and CoMSIA results can be modeled by combining MQS and chemical reactivity; in this context, these outcomes can be applied in QSAR correlations and docking studies and to gain a better understanding of the biological activity of a molecular set. Considerating that these approaches can be utilized when the receptor is known or unknown.

A.M.B thanks to the Fundación Universitaria Tecnológico Comfenalco.

1. Morales-Bayuelo A, Matute R A, Caballero J. New Insights from the CoMSIA Analysis within the Framework of Density Functional Theory. J Mol Model. 2015;21:156. https://bit.ly/3GLDQLs
2. Carbó-Dorca R, Arnau M, Leyda L. How similar is a molecule to another? An electron density measure of similarity between two molecular structures. Int J Quant Chem. 1980;17:1185. https://bit.ly/3mLwbVy
3. Amat L, Carbó-Dorca R. Use of promolecular ASA density functions as a general algorithm to obtain starting MO in SCF calculations. Int J Quant Chem. 2002;87:59. https://bit.ly/31zkJUX
4. Gironés X, Carbó-Dorca R. Modelling toxicity using molecular quantum similarity measures. QSAR Comb Sci. 2006;25:579. https://bit.ly/3BKbNbz
5. Carbó-Dorca R, Gironés X. New insights to understand the CoMFA and CoMSIA analysis within the framework of Density Functional Theory. Toward a generalized methodology. Int J Quat Chem. 2005;101:8.
6. Bultinck P, Rafat M, Ponec R, Gheluwe B V, Carbó-Dorca R, Popelier P. Electron Delocalization and Aromaticity in Linear Polyacenes: Atoms in Molecules Multicenter Delocalization Index. J Phys Chem A. 2006;110:7642. https://bit.ly/3GTyePd
7. Morales-Bayuelo A, Vivas-Reyes R. Theoretical model for the polarization molecular and Hückel treatment of PhosphoCyclopentadiene in an external electric field: Hirschfeld study. J Math Chem. 2013;51:1835. https://bit.ly/3COQ4AI
8. Morales-Bayuelo A, Vivas-Reyes R. Topological model to quantify the global reactivity indexes as local in Diels–Alder reactions, using density function theory (DFT) and local quantum similarity (LQS). J Math Chem. 2013;51:125. https://bit.ly/3wgMeOa
9. Parr R G, Yang W. Density Functional Theory of Atoms and Compounds; Oxford University Press: New York. 1989. https://bit.ly/3qa6Hn2
10. Geerlings P, De Proft F, Langenaeker W. Conceptual Density Functional Theory. Chem Rev. 2003;103:1793. https://bit.ly/3k60eW4
11. Carbó-Dorca R. Tagged sets, convex sets and quantum similarity measures. J Math Chem. 1998;23:353.
12. Kumar A, Siddiqi MI. CoMFA based de novo design of pyrrolidine carboxamides as inhibitors of enoyl acyl carrier protein reductase from Mycobacterium tuberculosis. J Mol Model. 2008 Oct;14(10):923-35. doi: 10.1007/s00894-008-0326-8. Epub 2008 Jul 15. PMID: 18626672.
13. Carbó-Dorca R. SM and ASA density functions, diagonal vector spaces and quantum chemistry. Adv Molec Simil. 1998;2:43-72.
14. Carbó-Dorca R, Gironés X. Foundation of quantum similarity measures and their relationship to QSPR: density function structure, approximations, and application examples. Int J Quant Chem. 2005;101:8. https://bit.ly/3q6lwGX
15. Alejandro Morales-Bayuelo, Juan Torres, Ricardo Vivas-Reyes. Hückel treatment of pyrrole and pentalene as a function of cyclopentadienyl using Local Quantum Similarity Index (LQSI) and the Topo-Geometrical Superposition Approach (TGSA). J Theoret Comp Chem. 2012;11:223. https://bit.ly/3bK2TAg
16. Hirshfeld FL. Bonded-atom fragments for describing molecular charge densities. Theor Chim Acta. 1977;44:129. https://bit.ly/3k7rkfN
17. De Proft F, Van Alsenoy C, Peeters A, Langenaeker W, Geerlings P. Atomic charges, dipole moments, and Fukui functions using the Hirshfeld partitioning of the electron density. J Comput Chem. 2002;23:1198.
18. Randic M, Johnson M A, Maggiora G M. In Concepts and Applications of Molecular Similarity, Design of Compounds with Desired Properties. Eds., Wiley-Interscience. New York. 1990;77.
19. Morales-Bayuelo A, Matute RA, Caballero J. Understanding the comparative molecular field analysis (CoMFA) in terms of molecular quantum similarity and DFT-based reactivity descriptors. J Mol Model. 2015 Jun;21(6):156. doi: 10.1007/s00894-015-2690-5. Epub 2015 May 28. PMID: 26016942.
20. Ayers P W, Anderson J S M, Bartolotti L J. Perturbative perspectives on the chemical reaction prediction problem. Int. J Quant. Chem. 2005;101:520. https://bit.ly/3EJtmun
21. Harbola MK, Chattaraj PK, Parr RG. Aspects of the Softness and Hardness Concepts of Density‐Functional Theory. Isr J Chem. 1991;31:395. https://bit.ly/3wjZRvW
22. Pearson RG. Chemical Hardness; Applications from Compounds to Solids; Wiley-VHC, Verlag GMBH: Weinheim, Germany. 1997.
23. Yang W T, Parr R G. Hardness, softness, and the fukui function in the electronic theory of metals and catalysis. Proc Natl Acad Sci. 1985;82:6723.
24. Chattaraj PK, Sarkar U, Roy DR. Update 1 of: electrophilicity index. Chem rev. 2006;106:2065. https://bit.ly/3wiZAJJ
25. Ayers P, Parr R G. Variational principles for describing chemical reactions: the Fukui function and chemical hardness revisited. J Am Chem Soc. 2000;122:2010. https://bit.ly/3mMoRcr
26. Galván M, Pérez P, Contreras R, Fuentealba P. Condensed-to-atoms electronic Fukui functions within the framework of spin-polarized density-functional theory. Chem Phys Lett. 1999;30:405.
27. Mortier W J, Yang W. The use of global and local molecular parameters for the analysis of the gas-phase basicity of amines. J Am Chem Soc. 1986;108:5708.
28. Fuentealba P, Pérez P, Contreras R. On the condensed Fukui function. J Chem Phys. 2000;113:2544.
29. Oliveira M, Cenzi G, Nunes RR, Andrighetti, Valadão D MS, Reis C, Oliveira Simões CM, Nunes RJ, Júnior MC, Taranto AG, Sanchez BAM. Viana GHR Varotti FP 2013 Molecules. 2013;18:15276.
30. Carbó-Dorca R. Mathematical aspects of the LCAO MO first order density function (5): centroid shifting of MO shape functions basis set, properties and applications. J Math Chem. 2013;51:289.
31. Carbó-Dorca R. Diagonal coefficient representation of density functions and quantum similarity measures. J Math Chem. 2008;44:621.
32. Becke AD. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys Rev A Gen Phys. 1988 Sep 15;38(6):3098-3100. doi: 10.1103/physreva.38.3098. PMID: 9900728.
33. GAUSSIAN 09, Revision C.01, Frisch M J, G. Trucks W, Schlegel H B, Scuseria G E, Robb M A, Cheeseman J R, Scalmani G, Barone V, Mennucci B, Petersson G A, Nakatsuji H, Caricato M, Li X, Hratchian HP, Izmaylov AF, Bloino J, Zheng G, Sonnenberg JL, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Vreven T, Montgomery JA Jr, Peralta JE, Ogliaro F, Bearpark M, Heyd JJ, Brothers E, Kudin KN, Staroverov V N, Keith T, Kobayashi R, Normand J, Raghavachari K, Rendell A, Burant JC, Iyengar SS, Tomasi J, Cossi M, Rega N, Millam JM, Klene M, Knox JE, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Martin RL, Morokuma K. Zakrzewski V G, Voth GA, Salvador P, Dannenberg JJ, Dapprich S, Daniels AD, Farkas O, Foresman JB, Ortiz JV, Cioslowski J, and Fox DJ, Gaussian, Inc., Wallingford CT. 2010.
34. Carbó-Dorca R, Besalú E, Amat L, Fradera X. Quantum molecular similarity measures (QMSM) as a natural way leading towards a theoretical foundation of quantitative structure-properties relationships (QSPR). J Math Chem. 1995;18:237.
35. Besalú E, Gironés X, Amat L, Carbó-Dorca R. Molecular quantum similarity and the fundamentals of QSAR. Acc Chem Res. 2002 May;35(5):289-95. doi: 10.1021/ar010048x. PMID: 12020166.
36. Boon G, Langenaeker W, De Proft F, De Winter H, Tollenaere JP, Geerlings PJ. Systematic study of the quality of various quantum similarity descriptors. Use of the autocorrelation function and principal component analysis. Phys Chem A. 2001;105:8805.