> Environmental Sciences. 2021 October 30;2(10):1059-1066. doi: 10.37871/jbres1348.
How the Chaos Theory is Defeated in the Yabu Meteorological Station, Cuba
Ricardo Oses Rodriguez1*, Claudia Osés Llanes2 and Rigoberto Fimia Duarte3
2Degree Specialist in Hygiene and Epidemiology, Subdirector of Hygiene and Epidemiology of Polyclinic, Cuba
3Faculty of Health Technology, University of Medical Sciences, Villa Clara Cuba
- Forecast
- Long term
- Time
- ROR model
- Chaos
Abstract
In this work, 8 weather variables were modeled at the Yabu meteorological station, Cuba, a daily database from the Yabu meteorological station, Cuba, of extreme temperatures, extreme humidity and their average value, precipitation, was used. The force of the wind and the cloudiness corresponding to the period from 1977 to 2021, a linear mathematical model is obtained through the methodology of Regressive Objective Regression (ROR) for each variable that explains their behavior, depending on these 15, 13, 10 and 8 years in advance. It is concluded that these models allow the long-term forecast of the weather, opening a new possibility for the forecast, concluding that the chaos in time can be overcome if this way of predicting is used, the calculation of the mean error regarding the forecast of persistence in temperatures, wind force and cloud cover, while the persistence model is better in humidity, this allows to have valuable information in the long term of the weather in a locality, which results in a better decision making in the different aspects of the economy and society that are impacted by the weather forecast. It is the first time that an ROR model has been applied to the weather forecast processes for a specific day 8, 10, 13 and 15 years in advance.
Introduction
In different fields of study, models of cumulative growth over time play an important role, many researchers have contributed to the knowledge of relevant developed models. There are some non-linear models, the most common Gompertz, Weibull, negative exponential, Richard's model, logistic, mono-molecular, Brody, Mitcherlich, von Betalanffy, S-Shaped among others, etc. There are about 77 equations referring to sigmoidal growth models which are used in epidemics, bioassays, agriculture, engineering fields, diameter of trees, distribution of forest height [1]. Among the most widely used growth models are those of Gompertz, Richard and Weibull. Their formulas can be seen in detail in Ban Ghanim Al-Ani [2], in this work a detailed and brilliant mathematical description of them is made, although the Root Mean Square Errors (RMSE) are large for non-linear models, These models were implemented in Covid-19, a new disease of which the behavior is known as time passes. Claudia was shown for the cases of Covid-19 in IRAQ that the ROR modeling gave better results than non-linear models, that is why for meteorological weather we will use this linear ROR model.
In our work we will develop a linear ROR model of 8 time variables, these are the extreme temperatures, maximum and minimum, the daily precipitation, the humidity, maximum and minimum, the daily average, the strength of the wind and the cloudiness and we will compare it with the persistence model, which is a good model obtained for weather forecasting, and we will demonstrate how it is possible to predict this on a certain day with enough time in advance that shows that chaos theory can be defeated if this way of predicting is used.
In an article about the 2021 Nobel Prize in Physics, it is said verbatim about mathematical models for weather forecasting:
These models are based on the laws of physics and have been developed from models that were used to predict the weather. Weather is described by meteorological quantities such as temperature, precipitation, wind or clouds, and is affected by what happens in the oceans and on land. Climate models are based upon the weather’s calculated statistical properties, such as average values, standard deviations, highest and lowest measured values, etcetera. They cannot tell us what the weather will be in Stockholm on 10 December next year, but we can get some idea of what temperature or how much rainfall we can expect on average in Stockholm in December.
In this appointment the knowledge that until now is had of chaos and its impossibility of going beyond 10 days with the help of predictive weather models is evidenced, however according to Brigitte Boisselier, PhD in Physics, Professor of Biochemistry, Director of Clonaid ¨ When a relatively elderly, eminent and distinguished scientist declares that something is possible, he is probably right. When it coincides that something is impossible, there is a high probability that it is wrong.
We could not count on the history of the data from December 10 in Stockholm, however we have the data from Yabu station for that day through the years and it is with these data that we will prove that the long-term weather forecast for 1 This particular day is also possible with an acceptable margin of error, which shows that chaos can be overcome if this way of predicting is used.
Materials and Methods
For this work the data of 8 weather variables were used, these are the extreme temperatures, maximum and minimum, the daily precipitation, the maximum and minimum humidity, the daily average humidity, the strength of the wind and the cloudiness. The forecast was made with the use of the Regressive Objective Regression (ROR) methodology that has been implemented in different variables such as viruses that circulate in the province of Villa Clara and particularly in Covid-19 in Cuba [3-6]. A long-term forecast was made up to 15 years from December 10, 2020 to December 10, 2035.
In this linear ROR methodology, the dichotomous variables DS, DI and NoC must first be created, where: NoC: Number of base cases (its coefficient in the model represents the trend of the series). DS = 1, if NoC is odd; DI = 0, if NoC is even, and vice versa. DS represents a sawtooth function and DI this same function, but in an inverted way, in such a way that the variable to be modeled is trapped between these parameters and a large amount of variance is explained, a detailed explanation of it can be seen in [7]. In figure 1 the location of the meteorological stations of Villa Clara, Cuba.
Climate
General description: According to the Köppen classification (modified), in most of Cuba the predominant climate is of the warm tropical type, with a rainy season in the summer. In general, it is quite accepted to express that the climate of Cuba is tropical, seasonally humid, with maritime influence and semi-continental features, our province of Villa Clara also responds to these characteristics. As determining factors in the formation of the climate, the amount of solar radiation received, the particularities of the atmospheric circulation over the country, and the different influence of the physical-geographical characteristics of the territory are identified. Due to its geographical position, our city is located at a latitude very close to the Tropic of Cancer, which conditions the reception of high values of solar radiation throughout the year, determining the warm character of its climate. In addition, it is located on the border between the zones of tropical and extratropical circulation, receiving the influence of both on a seasonal basis. In the season that goes approximately from November to April, weather and climate variations become more noticeable, with abrupt changes in daily weather, associated with the passage of frontal systems, the anticyclonic influence of continental origin and low centers. Extratropical pressures, from May to October, on the contrary, there are few variations over time, with the more or less marked influence of the North Atlantic Anticyclone. The most important changes are related to the presence of disturbances in the tropical circulation (eastern waves and tropical cyclones).
Everything was done with the help of the SPSS Statistical Package, Version 19, from the IBM company. The objective of this work is aimed at predicting long-term weather variables in El Yabú Cuba and thus defeating chaos theory.
Results and Discussion
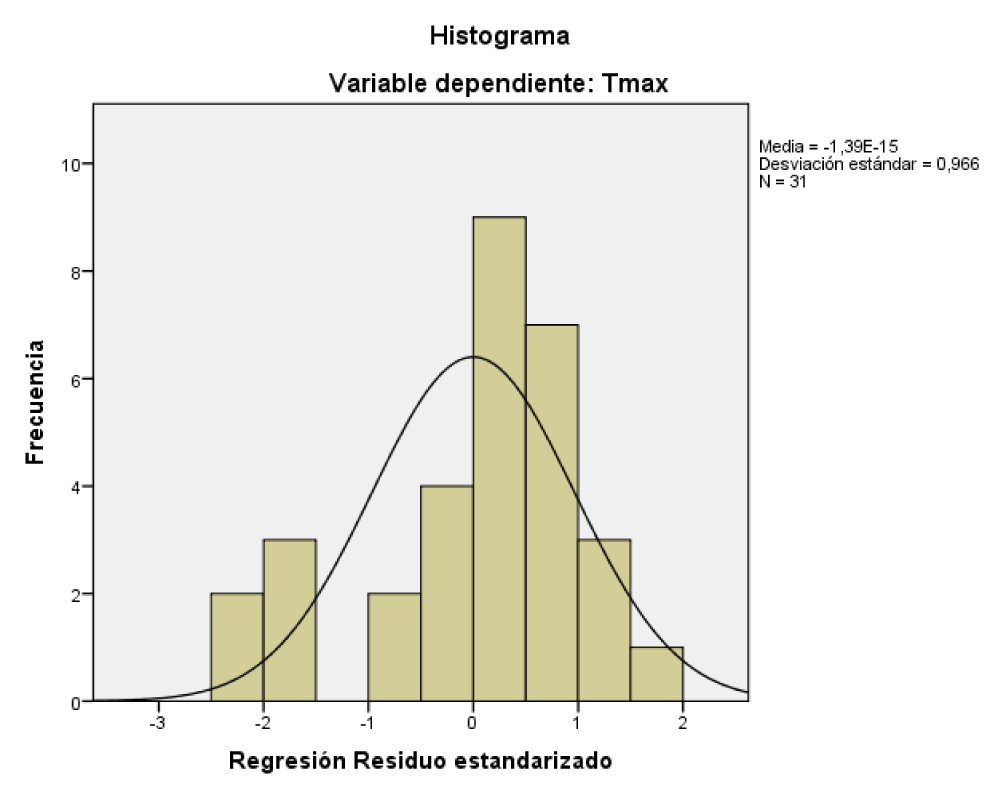
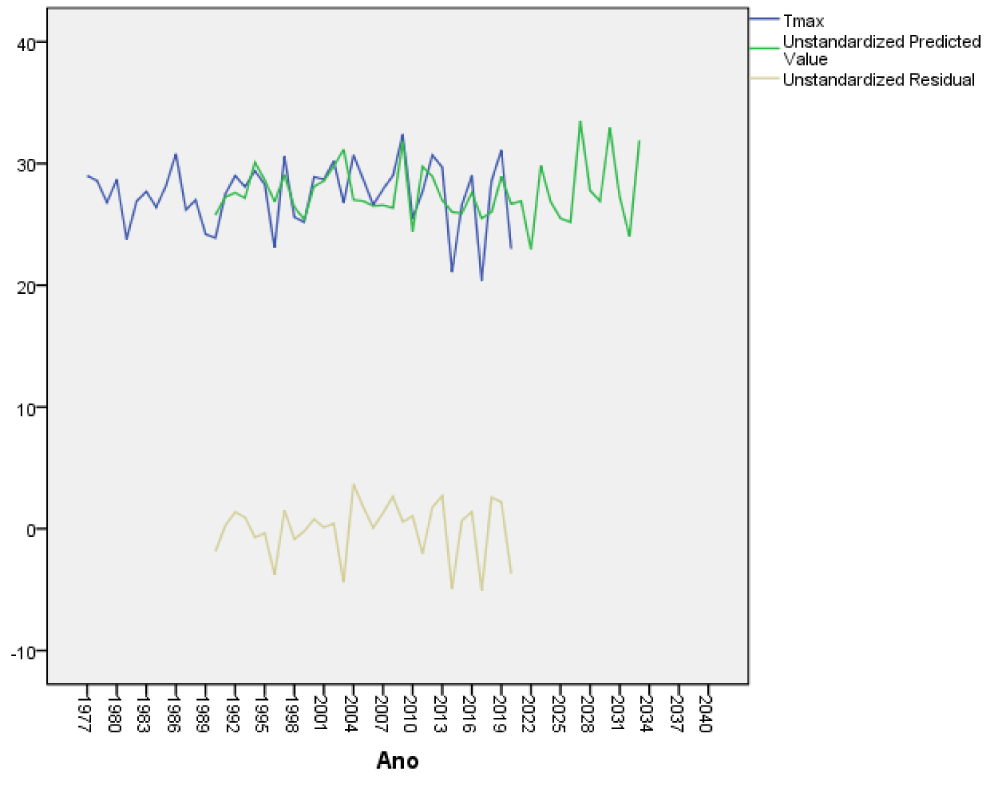
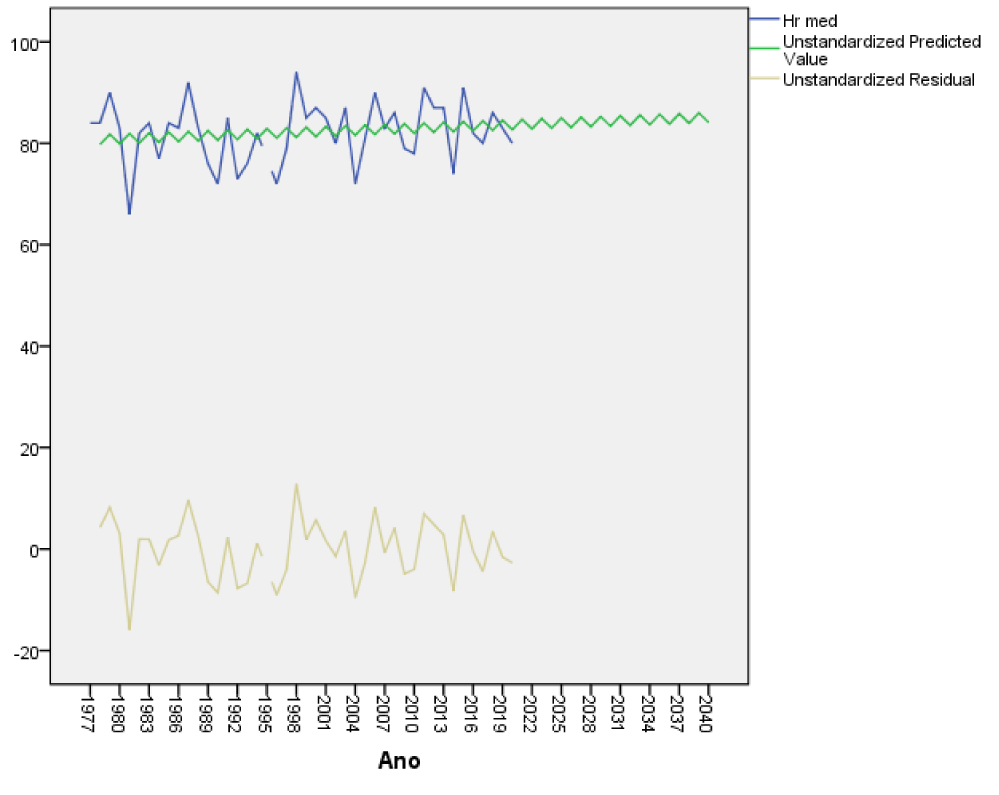
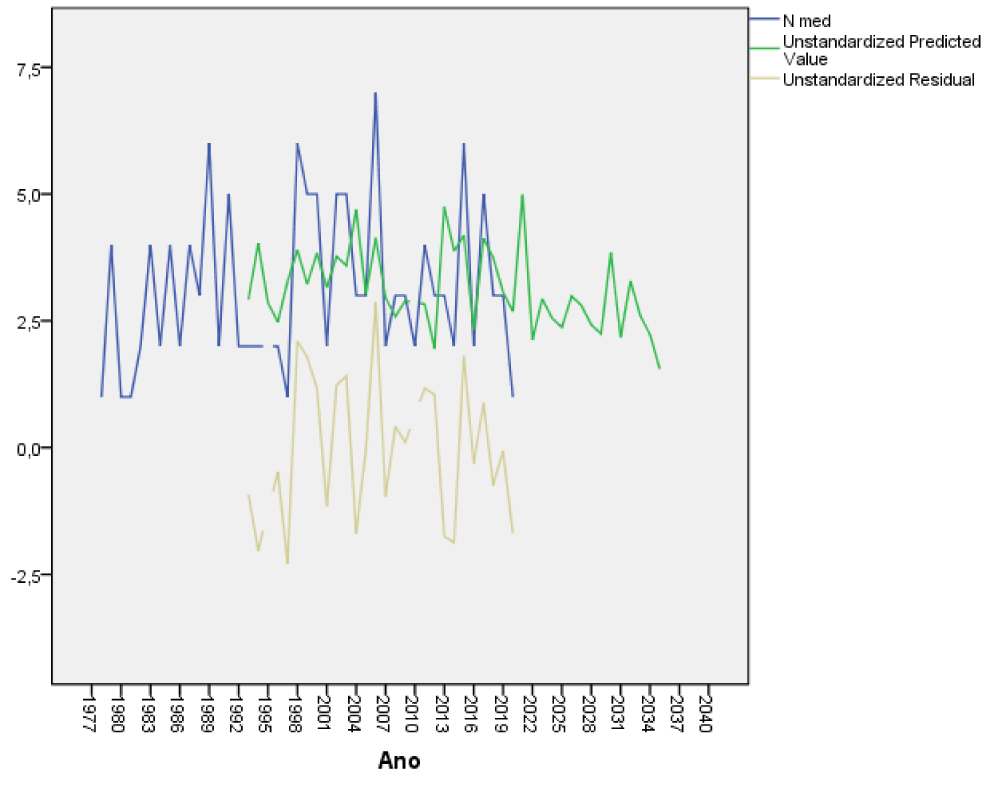
In table 1, you can see the parameters of the models. The coefficients of the explained variance R are high, the errors of the models are small, the temperatures depend on the lags in 15 years the minimum and 13 years the maximum, the precipitation of 8 years ago, the minimum humidity of 10 years ago, the Wind force (FF) in 13 years ago and cloud cover in 15 years ago. In table 2, a summary of the linear ROR model obtained by variable, this explains 99.7% of the variance with an error of 2.41ºC, which is a small error considering that we are predicting the maximum daily temperature 13 years in advance. Table 3 shows the analysis of variance of the model, which is highly significant with a Fisher's F of 1350.6 significant at 100%. In table 4, it can be seen that all the variables are significant, the temperature trend is not significant and that is why it is not shown. The linear model depends on the data returned in 13 years (Lag13 Tmax). In figure 2 we can see that the residuals do not differ from a normal distribution with zero mean and 0.966 standard deviation. In figure 3, the modeling results can be seen that the predicted values coincide with the real values of the variable, the errors are very small, close to zero.
| Table 1: Parameters of the models of different time variables in Yabú Cuba. | |||||||
| Variable | R | Error of the model | Saw Tooth (DS) | Inverted Saw Tooth (DI) | Tend | Delay Coeficient |
Fisher F |
| T Min | 98.8 | 3.09 | 10.73 | 8.86 | 15 0.472 |
335 | |
| T max | 99.7 | 2.41 | 51.08 | 49.93 | 13 -0.833 |
1350 | |
| Precip | 100 | 0.0 | -8 E(-16) | -1.5E(-15) | 2.98E(-17) | 8 -5.8E (-17) |
7.51i |
| HRx | 100 | 1.92 | 96.44 | 96.11 | 0.041 | 36861 | |
| Hrn | 98.7 | 9.80 | 77.99 | 73.77 | -0.054 | 10 -0.333 |
277 |
| Hrm | 99.7 | 6.16 | 81.57 | 79.62 | 0.070 | 2490 | |
| FF | 90.2 | 2.91 | 2.353 | 2.586 | 0.049 | 13 0.261 |
27.2 |
| Nubosidad | 92.4 | 1.55 | 2.98 | 2.634 | 15 0.496 |
32.2 | |
| Table 2: Model summaryc.d. | |||||
| Model | R | R Squaredb | R Squared adjusted | Stándard error of estimation | Durbin-Watson |
| 1 | 0.997a | 0.993 | 0.992 | 2.4144 | 2.503 |
| a. Predictors: Log13Tmax. DS. DI b. For the regression through the origin (the model without interception). R squared measures the proportion of the variability in the dependent variable on the origin explained by the regression. This cannot be compared to R squared for models that include intercept. c. Dependent variable: Tmax d. Linear regression through the origin |
|||||
| Table 3: ANOVAa.b. | ||||||
| Model | Sum of Squares | Df | Quadratic mean | F | Sig. | |
| Regressión | 23618.784 | 3 | 7872.928 | 1350.618 | 0.000c | |
| Residuals | 163.216 | 28 | 5.829 | |||
| Total | 23782.000d | 31 | ||||
| a. Dependent variable: Tmax | ||||||
| b. Linear regression through the origin | ||||||
| c. Predictors: Lag13Tmax. DS. DI | ||||||
| d. This total sum of squares is not corrected for the constant because the constant is zero for the regression through the origin. | ||||||
| Table 4: Coefficientsa.b. | ||||||
| Model | Unstandardized Coefficients | Standardized Coefficients | t | Sig. | ||
| B | Error standing | Beta | ||||
| DS | 51.079 | 6.010 | 1.283 | 8.499 | .000 | |
| DI | 49.939 | 5.930 | 1.295 | 8.422 | .000 | |
| Log13Tmax | -.833 | .216 | -.831 | -3.864 | .001 | |
| a. Dependent variable: Tmax | ||||||
| b. Linear regression through the origin | ||||||
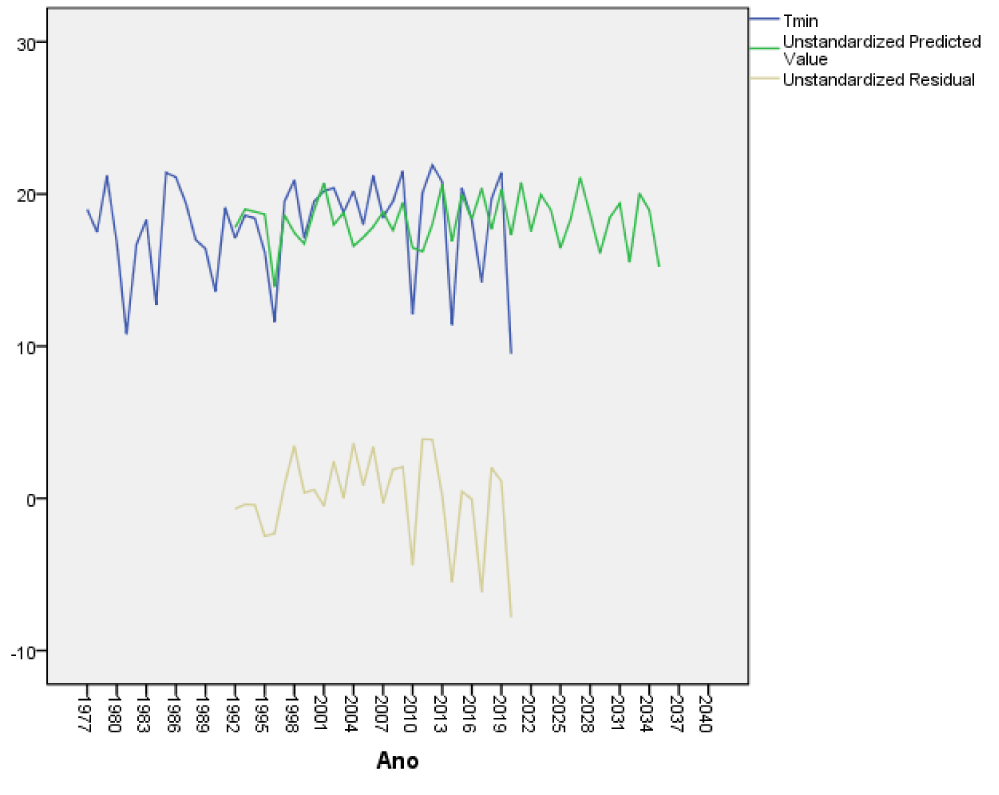
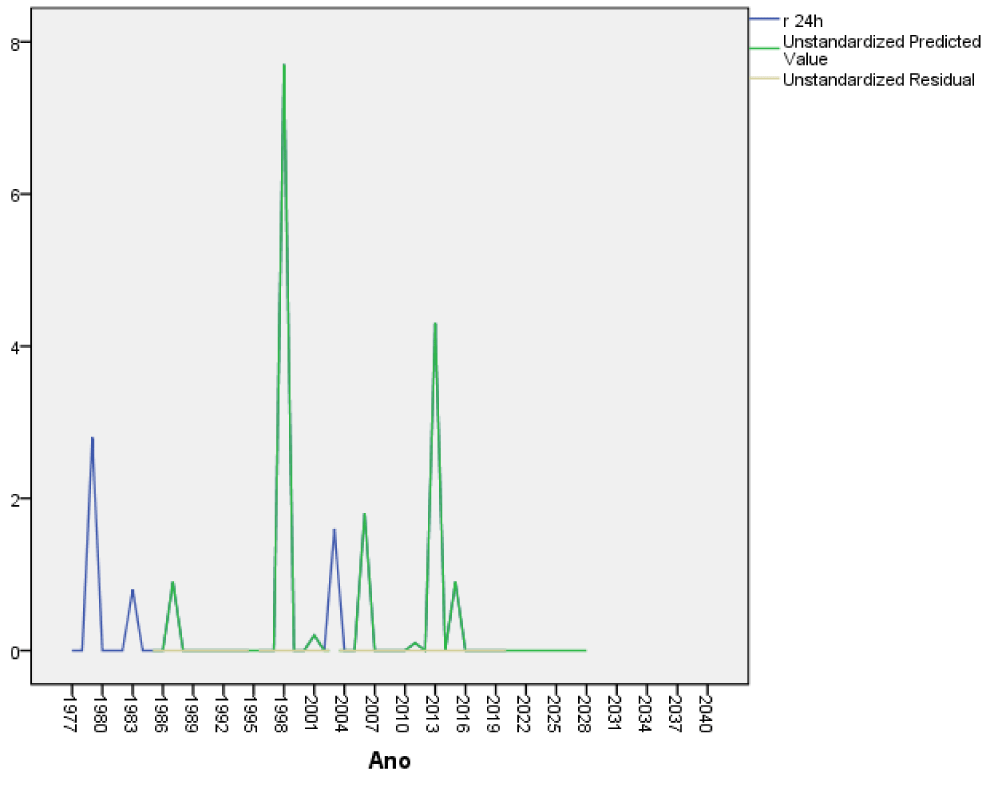
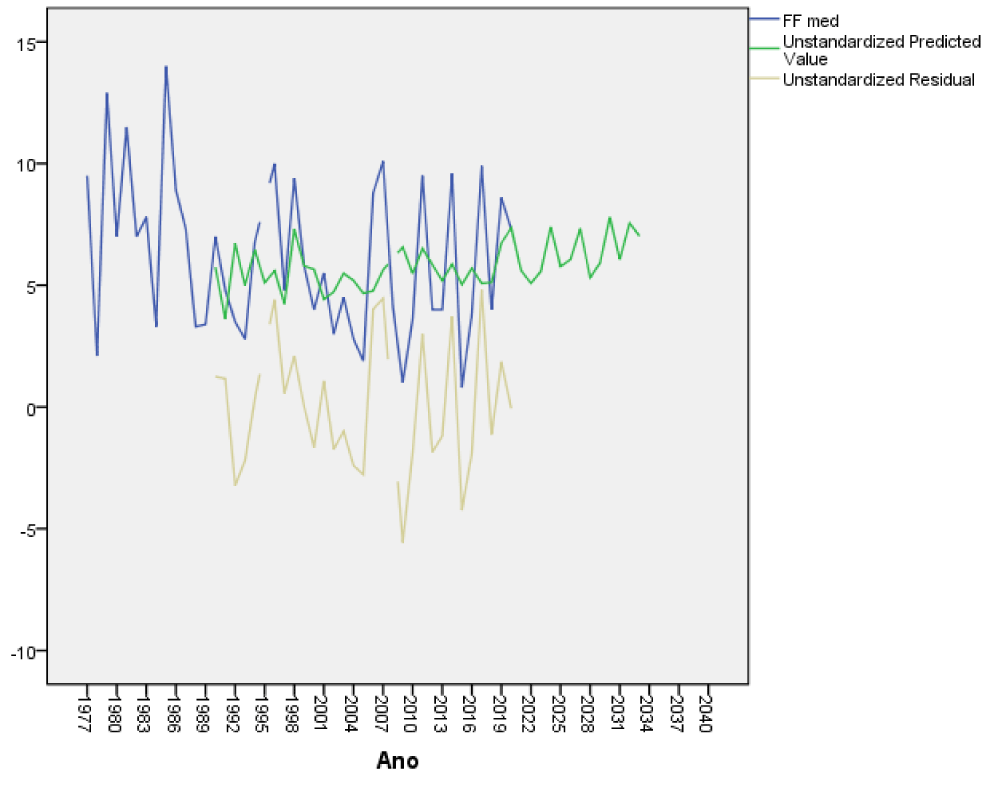
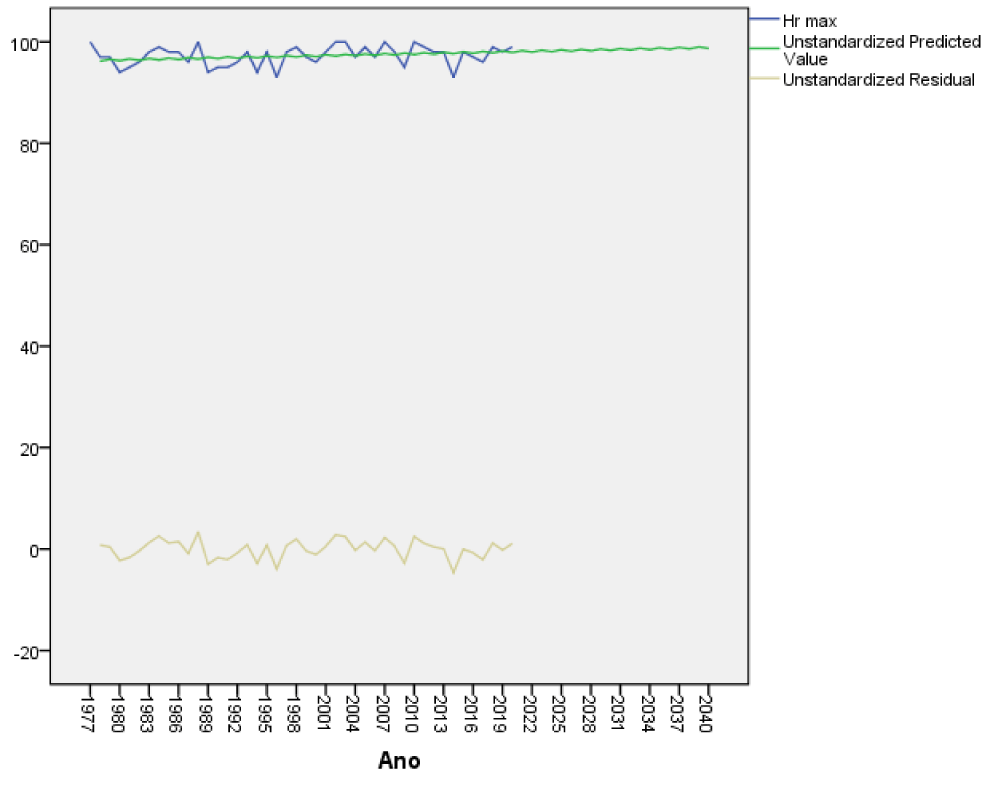
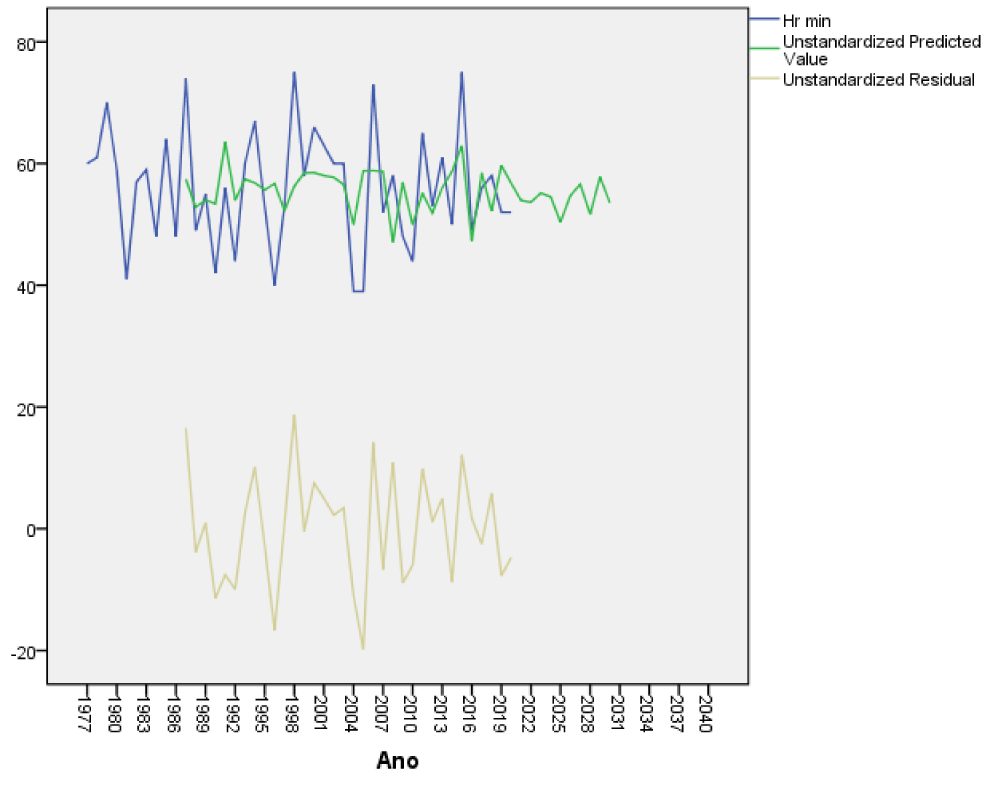
As in extreme temperatures no trend was observed, we can affirm that on December 10 throughout history there is no cooling or warming trend, which does not mean that for some other day in particular from the daily data series there may be a significant trend. The forecast 13 years in advance is shown in table 5, it can be seen that December 10 will present days with high and less high maximum temperatures. It is the first time that an ROR model has been applied to the long-term forecast of the weather in Cuba 13 years in advance for a specific day, as this had been done for climatic variables such as the dumping of sand on Varadero Beach with good results (Oses et al 2021), also for electricity consumption in the province [8,9] in addition, in other works the number of people is also modeled in the long term with cerebrovascular accidents, models the atmospheric pressure and its impact on the density of mosquitoes well in advance. Another long-term model was enthroned in Sancti Spiritus Cuba where a forecast of daily variables is made one year in advance using the ROR regression [10]. Table 6 shows the results of the errors taking an independent sample of 11 cases from 2010 to 2021 to see how the model works in an independent sample of 25% of the cases. As can be seen, the errors are small for all the variables as well as the standard deviations of the variables. The results of the forecast for the rest of the weather variables in Yabu, Cuba will be shown in figures 4-10.
| Table 5: Case summary. | ||||||
| Yeari | Month | Day | Maximun Temperature(Tmax) | Unstandardized Predicted Value | Unstandardized Residual | |
| 1 | 1977 | 12 | 10 | 29.0 | . | . |
| 2 | 1978 | 12 | 10 | 28.6 | . | . |
| 3 | 1979 | 12 | 10 | 26.8 | . | . |
| 4 | 1980 | 12 | 10 | 28.7 | . | . |
| 5 | 1981 | 12 | 10 | 23.8 | . | . |
| 6 | 1982 | 12 | 10 | 26.9 | . | . |
| 7 | 1983 | 12 | 10 | 27.7 | . | . |
| 8 | 1984 | 12 | 10 | 26.4 | . | . |
| 9 | 1985 | 12 | 10 | 28.2 | . | . |
| 10 | 1986 | 12 | 10 | 30.8 | . | . |
| 11 | 1987 | 12 | 10 | 26.2 | . | . |
| 12 | 1988 | 12 | 10 | 27.0 | . | . |
| 13 | 1989 | 12 | 10 | 24.2 | . | . |
| 14 | 1990 | 12 | 10 | 23.9 | 25.77404 | -1.87404 |
| 15 | 1991 | 12 | 10 | 27.5 | 27.24671 | .25329 |
| 16 | 1992 | 12 | 10 | 29.0 | 27.60726 | 1.39274 |
| 17 | 1993 | 12 | 10 | 28.1 | 27.16338 | .93662 |
| 18 | 1994 | 12 | 10 | 29.4 | 30.10712 | -.70712 |
| 19 | 1995 | 12 | 10 | 28.3 | 28.66329 | -.36329 |
| 20 | 1996 | 12 | 10 | 23.1 | 26.85731 | -3.75731 |
| 21 | 1997 | 12 | 10 | 30.6 | 29.07994 | 1.52006 |
| 22 | 1998 | 12 | 10 | 25.6 | 26.44067 | -.84067 |
| 23 | 1999 | 12 | 10 | 25.2 | 25.41348 | -.21348 |
| 24 | 2000 | 12 | 10 | 28.9 | 28.10724 | .79276 |
| 25 | 2001 | 12 | 10 | 28.7 | 28.57996 | .12004 |
| 26 | 2002 | 12 | 10 | 30.2 | 29.77380 | .42620 |
| 27 | 2003 | 12 | 10 | 26.8 | 31.16315 | -4.36315 | |
| 28 | 2004 | 12 | 10 | 30.7 | 27.02397 | 3.67603 | |
| 29 | 2005 | 12 | 10 | 28.7 | 26.91340 | 1.78660 | |
| 30 | 2006 | 12 | 10 | 26.6 | 26.52399 | .07601 | |
| 31 | 2007 | 12 | 10 | 27.9 | 26.58008 | 1.31992 | |
| 32 | 2008 | 12 | 10 | 29.0 | 26.35734 | 2.64266 | |
| 33 | 2009 | 12 | 10 | 32.4 | 31.82978 | .57022 | |
| 34 | 2010 | 12 | 10 | 25.5 | 24.44078 | 1.05922 | |
| 35 | 2011 | 12 | 10 | 27.7 | 29.74656 | -2.04656 | |
| 36 | 2012 | 12 | 10 | 30.7 | 28.94052 | 1.75948 | |
| 37 | 2013 | 12 | 10 | 29.7 | 26.99672 | 2.70328 | |
| 38 | 2014 | 12 | 10 | 21.1 | 26.02402 | -4.92402 | |
| 39 | 2015 | 12 | 10 | 26.6 | 25.91345 | .68655 | |
| 40 | 2016 | 12 | 10 | 29.0 | 27.60726 | 1.39274 | |
| 41 | 2017 | 12 | 10 | 20.4 | 25.49681 | -5.09681 | |
| 42 | 2018 | 12 | 10 | 28.6 | 26.02402 | 2.57598 | |
| 43 | 2019 | 12 | 10 | 31.1 | 28.91328 | 2.18672 | |
| 44 | 2020 | 12 | 10 | 23.0 | 26.69065 | -3.69065 | |
| 45 | 2021 | 12 | 10 | . | 26.91340 | . | |
| 46 | 2022 | 12 | 10 | . | 22.94087 | . | |
| 47 | 2023 | 12 | 10 | . | 29.82989 | . | |
| 48 | 2024 | 12 | 10 | . | 26.85731 | . | |
| 49 | 2025 | 12 | 10 | . | 25.49681 | . | |
| 50 | 2026 | 12 | 10 | . | 25.19074 | . | |
| 51 | 2027 | 12 | 10 | . | 33.49634 | . | |
| 52 | 2028 | 12 | 10 | . | 27.77392 | . | |
| 53 | 2029 | 12 | 10 | . | 26.91340 | . | |
| 54 | 2030 | 12 | 10 | . | 32.94029 | . | |
| 55 | 2031 | 12 | 10 | . | 27.24671 | . | |
| 56 | 2032 | 12 | 10 | . | 24.02414 | . | |
| 57 | 2033 | 12 | 10 | . | 31.91310 | . | |
| 58 | 2034 | 12 | 10 | . | . | . | |
| 59 | 2035 | 12 | 10 | . | . | . | |
| 60 | 2036 | 12 | 10 | . | . | . | |
| 61 | 2037 | 12 | 10 | . | . | . | |
| 62 | 2038 | 12 | 10 | . | . | . | |
| 63 | 2039 | 12 | 10 | . | . | . | |
| 64 | 2040 | 12 | 10 | . | . | . | |
| Total | N | 64 | 64 | 64 | 44 | 44 | 31 |
| a. Limited to the first 100 cases. | |||||||
| Table 6: Mean errors of the time variables for an independent sample of 11 cases starting in 2010. | |||||
| N | Mínimal | Máximal | Media | Deviation Standing | |
| eTmin.mi | 11 | -7.82 | 3.89 | -1.1261 | 4.12549 |
| eTmax.mi | 11 | -5.10 | 2.70 | -.3086 | 3.03874 |
| er24h.mi | 11 | .00 | .00 | .0000 | .00000 |
| eFFmed.mi | 11 | -4.23 | 4.83 | .1066 | 2.84084 |
| eHrmax.mi | 11 | -4.65 | 2.51 | -.1206 | 1.92130 |
| eHrmin.mi | 11 | -8.74 | 12.10 | .5386 | 7.09060 |
| eHrmed.mi | 11 | -8.28 | 6.97 | .3082 | 5.00155 |
| eNmed.mi | 10 | -1.87 | 1.81 | -.1527 | 1.34801 |
| N válid (per list) | 10 | ||||
Finally, the improvement index of one model over another was calculated as follows, which is nothing more than the modeling SKILL.
Here a slight modification was made to the formula [11-14] by adding the mean instead of the mean squared error (MSE) according to the original formula, obtaining that the established model is the persistence model and the model to be checked is the ROR, this was done in the independent sample of 11 cases in table 7.
| Table 7: Sample. | |||
| Variable | Error ROR | Error Persistency | Improvement (%) |
| Temperature Minimun (T Min). | -1.1261 | -1.3175 | 14.5 |
| Temperature Máximum (T max) | -0.3086 | -0.7757 | 60.2 |
| Precipitation | 0.000 | 0.000 | - |
| Maximum Relative Humidity (HRx) | -0.1206 | -0.1105 | * |
| Mínimum Relative Humidity (Hrn) | 0.5386 | 0.5250 | * |
| Mean Relative Humidity (Hrm) | 0.3082 | 0.2002 | * |
| Mean velocity of wind (FF) | 0.1066 | 0.1786 | 40.31 |
| Cloudiness | -0.1527 | -0.3736 | 59.12 |
The improvement ranges from 14.5% in the minimum temperature to 60.2% in the maximum, so we can affirm that in this case a linear ROR model exceeds a persistence model in most of the variables studied except for humidities where persistence exceeds to the ROR model by a narrow margin.
Conclusion
The coefficients of the explained variance R are high, the errors of the models small, the temperatures depend on the delays in 15 years the minimum and 13 years the maximum, the precipitation of 8 years ago, the minimum humidity of 10 years ago, the Wind force (FF) in 13 years ago and cloud cover in 15 years ago.
Depending on the meteorological variable studied, which shows that what will happen in a day can be predicted well in advance, thus defeating the chaos in the weather forecast. In the independent sample of 11 years the errors are small for all the variables as well as the standard deviations of the variables. The improvement ranges from 14.5% in the minimum temperature to 60.2% in the maximum, so we can affirm that in this case a linear ROR model exceeds a persistence model in most of the variables studied except for humidities where persistence exceeds to the ROR model by a narrow margin. It is the first time that an ROR model has been applied to the weather forecast processes for a specific day 8, 10, 13 and 15 years in advance.
Acknowledgment
We would like to thank the Villa Clara Cuba Provincial Meteorological Center for providing the computing resources without which this work would not have been possible, as well as Arch. Odalys D. Llanes Concepcion for editing the document.
References
- Dagogo J, Nduka EC, Ogoke. Comparative analysis of richards, gompertz and weibull models. IOSR Journal of Mathematics. 2020;16(1):15-20. https://tinyurl.com/nkxffwz6
- Ghanim AA. Statistical modeling of the novel COVID-19 epidemic in Iraq. Epidemiologic Methods. 2020. https://tinyurl.com/4k6tsuxt
- Álvarez ML, Rodríguez R, Fimia DR, Rodríguez BC, Iannacone J, Zaita F. The regressive objective regression is more than just a blanket for viruses circulating in the province of Villa Clara, Cuba. The Biologist. 2017;15:127.
- Rodríguez, Llanes, Duarte, Meneses, Iannacone, Santos, Wilford G. Age prediction for covid-19 suspects and contacts in villa clara province, cuba age prediction. 2021;6(4):41-51. https://tinyurl.com/fr3js658
- Rodríguez, Duarte, Llanes, Gavilanes, Zambrano, González M. Forecast of new and deceased cases of covid-19 in cuba with an advance of 105 days. Acta Scientific Sciences. 2021;3(7):31-36. https://tinyurl.com/9km24scs
- Rodriguez, Martinez. Mathematical modeling and forecast 11 years in advance of the dumping of sand in varadero beach, cuba, using the regressive objective regression (ROR) methodology. Journal of Engineering and Applied Sciences Technology. 2021;3(1):1-3. https://tinyurl.com/4j7789k6
- Fimia RD, Rodríguez RO, González, Contreras M, Martín M. The killer whale entomaphones and copepods of biological control alternatives have mathematical modeling in Cuba's central provinces. Anales de la Academia de Ciencias de Cuba. 2020;10(3).
- Rodríguez, Fernández, González, Duarte. Studio of provincial provincial electric consumption of villa clara and its province 2019-2023 cuba. Scientific Review of Renewable Energy Resources. 2018.
- Ricardo Oses Rodríguez, Humberto Machado Fernández, González, Duarte. Studio of electric consumption of cala of villa clara and its prostitutional diario in largo plazo 2019-2020. Cuba. Scientific review of renewable energy sources. 2019.
- Rodríguez, Duarte, González, Martínez, Cabrera, Padrón. Long term forecast of meteorological variables in sancti spiritus. Cuba applied ecology and environmental sciences. 2014;2(1):37-42. https://tinyurl.com/y8cxhhtr
- Wilks SD. Statistical methods in the atmospheric sciences. An introduction. International Geophysics Series. 1987;59:255- 256. https://tinyurl.com/2b7h32pn
- Rodríguez, Freyre, Duarte, Llanes, Aleman, Gálvez, Martinez, Marrero. Modulatión of the quantity of deceased and revenues for stroke in sagua la grande, villa clara, cuba. Impact of the climate. 2019;7(2).
- Duarte, Rodríguez, Elbal, Wilfrido Cárdenas, Boffill, Pedro. In function of mathematical modeling and atmospheric pressure in villa clara, cuba. Revista De La Facultad De Medicina De La Universidad Nacional De Colombia. 2020.
- Llanes CO, Rodríguez RO, Duarte RF, Gavilanes MPZ, Wilford. Comparison of linear ROR vs non linear weibull model for COVID-19 in Iraq. HJAMR. 2020;2(5). https://tinyurl.com/a8yzmkz
Content Alerts
SignUp to our
Content alerts.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.