A New Model of Consciousness as a Quantum Field

The article proposes a new model of consciousness of living organisms, based on an extension of the de Broglie-Bohm theory, which is also meeting the principles of the Quantum Field Theory. In particular, the article starts from the consideration that living organisms are similar to open systems, operating far from the thermodynamic equilibrium: in fact, they are subjected to continuous internal flows and exchanges of energy, matter and information with the surrounding environments. On a deeper physical level, however, these exchanges are mediated by quantum wave oscillations and interactions, so that it is argued that living organisms are even operating far from quantum equilibrium. Therefore, leveraging on a prior art arguing that quantum theory might be a special case of a much wider physics, where systems are far from quantum equilibrium, the article proposes a wider perspective of the de Broglie-Bohm theory for modeling consciousness. Consciousness is modelled as a special quantum wave field whose associated potential is elaborated as active information by living organism and accounts, with different complexity levels, for consciousness phenomena in life. Moreover, the article proposes that the form or curvature of the consciousness wave field can be expressed in terms of Nambu Goldstone bosons condensations (as described in Quantum Field Theory) associated to symmetry breaking phenomena in living organisms.

Living organisms, from a physical perspective, can be modeled as open systems, operating far from thermodynamic equilibrium. In fact, life is based on internal flows and exchanges of energy, matter, and information with the surrounding environment. In fact, this high-level model is compliant with the definition of dissipative structures as proposed by Nobel Prize Ilya Prigogine.

Moving the analysis on the deeper physical level, these exchanges of living organisms are mediated by wave-like quantum vibrations including, for example, mechanical, electromagnetic, nuclear and thermal ones. Even the vacuum, according to Quantum Field Theory (QFT), is an arena of quantum fluctuations which represent a ground state of energy. All these quantum vibrations and oscillations create, through complex interference patterns, a continuum of quantum fields capable of shaping matter’s structure, coherence levels and, as such, various biological functionalities [1-3] and consciousness.

As a matter of fact, several research efforts have been made for modelling life dynamics with Quantum Mechanics (QM). One of the first remarkable examples is dated 1944 when E. Schrodinger wrote his book, “What is life?” Another example is the pioneering research activities of Fröhlich H who demonstrated that the concept of quantum coherence is an inherent property of living cells: for instance, long-range interactions are used for synchronization of cell division processes. This avenue of research has been progressed by several activities, experiments and publications [4-8] and, more recently, it has been confirmed also by new advances in quantum biology [9-11].

Therefore, it seems to be reasonable arguing that living organisms should be considered open systems not only from far thermodynamic equilibrium (i.e., dissipative structures) but also far from the quantum equilibrium. If so, life and, consequently of consciousness, should be modelled through of a wider approach than Quantum Mechanics and QFT (which are mainly considering systems on the quantum equilibrium): in particular, this new approach should be capable of addressing systems dynamics beyond quantum equilibrium, accounting for quantum phenomena (e.g., entanglement) even at the ambient temperatures in living organisms.

Starting from these considerations, this article proposes an unpublished model of consciousness of living organisms, based on an extension of the de Broglie-Bohm theory, which is also meeting the principles of the Quantum Field Theory. In fact, leveraging on a prior art arguing that quantum theory might be a special case of a much wider physics [12], where systems are far from quantum equilibrium, the article proposes a novel perspective of the de Broglie-Bohm theory for modeling consciousness of living organisms.

De Broglie’s theory asserts that any quantum particle has an accompanying field that together form a single quantum system. The quantum field accompanying matter is commonly called the wave field and evolves in time according to the Schrodinger equation. The central concept of this theory is that the dynamics of matter is causally governed by its wave field. De Broglie’s pilot-wave theory was resumed in 1952 by Bohm D, who noted that the theory is non-local: this led to the development of the concept of quantum potential and active information.

These concepts have been considered also by [13], where Authors re-interpreted the Eccles’ proposal of a mind-field in light of the de Broglie - Bohm theory. Before that, Eccles [14] proposed that quantum processes may be important in understanding the activities of the brain: specifically, following a suggestion by Margenau [15], Eccles postulated the idea of a “mind-field”. In [13] this mind-field is considered containing active information as quantum potential.

The main novelty of the article is proposing to model consciousness as a generalized quantum wave field, whose associated potential is elaborated as active information by living organism and accounts, with different complexity levels, for consciousness phenomena in life.

As for the quantum field (and unlike a classical field) the consciousness quantum wave field has no classical sources and its form or curvature has more importance, from a physical perspective, than its amplitude. In particular, the article also argues (for the first time) that this curvature is the active information that can be expressed in terms of Nambu Goldstone bosons condensations (as described in Quantum Field Theory) associated to symmetry breaking phenomena in living organisms.

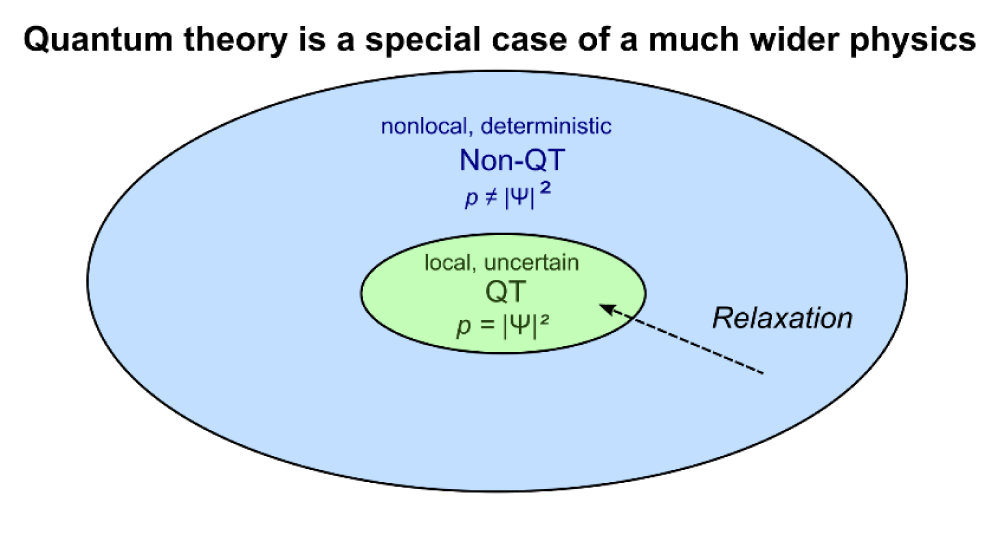
It should be mentioned that the quantum potential (in the current de Broglie-Bohm theory) could be considered as a special subset of the consciousness potential described by this paper. From an ontological viewpoint, this is in line with is argued by Antony Valentini: quantum theory emerges as a special subset of a wider physics dealing with systems far from quantum equilibrium as living organisms. In figure 1 a diagram is reported made by Antony Valentini in a lecture about the De Broglie–Bohm theory [16].

Figure 1: Diagram made by Antony Valentini in a lecture about the De Broglie-Bohm theory [16]: with p is representing the probability density function and 𝞧 is the wave function.

In summary, the main novelties of this article are contained in the following contributions:

1. The unpublished application of a wider quantum approach for modelling life and consciousness, based on the fact that living organisms are beyond quantum equilibrium;
2. A new model of consciousness as a generalized quantum wave field, which is extending the current concept of quantum field of the de Broglie-Bohm theory. The associated consciousness potential, which is processed as active information by living organism, accounts, with different complexity levels, for all consciousness phenomena in life;
3. The idea that the form or curvature of the consciousness quantum wave field can be expressed in terms of Nambu Goldstone bosons condensations, thus creating a bridge between the de Broglie-Bohm theory and QFT for living organisms.

We recall that according to the theory of de Broglie particle motions are determined by the wave function, called a pilot wave, which is following the Schrodinger equation. In 1952, Bohm D resumed the pilot wave theory and applied it for quantum measurements: he demonstrated that the outcome of a measurement on one particle can depend on macroscopic operations (accounting for the so-called hidden variables) performed on a distant particle instantaneously (non-locality).

Also, Bell J contributed to this research avenue arguing that the pilot wave is a real field, and not merely a mathematical object or probability wave. Therefore, as well pointed out in [12], pilot-wave theory is based on the concept of action-at-a-distance: the outcome of a quantum measurement on one particle can depend on macroscopic operations performed on a distant particle. In other words, pilot-wave theory gives the same observable results as conventional quantum theory if the initial particle positions have a standard Born-rule distribution, which is an equilibrium condition.

It is recalled that the Born rule (formulated by Max Born in 1926) is a key postulate of quantum mechanics: in its simplest form, it states that the probability distribution of finding a particle at a given point, when measured, is proportional to the squared amplitude of the wavefunction. Nevertheless, in de Broglie pilot-wave theory, the quantum equilibrium distribution – according to the Born rule-is only a special case.

The theory allows also other quantum non-equilibrium distributions. Bohm D, as well as other physicists after him, have tried to provide evidence that the Born rule is not representing a basic law, but rather a hypothesis (called quantum equilibrium hypothesis) which applies when a quantum equilibrium is reached during the course of the time development under the Schrödinger equation. Therefore, as previously mentioned, Valentini A [12] argued that the quantum theory might be a special case of a much wider physics, where the quantum equilibrium distribution – according to the Born rule-is only a special case. This allows non-local signals and violation of the uncertainty principle (which prevents simultaneous measurements of position and momentum). In other words, at the equilibrium, the possibility of superluminal signaling fades away and statistical uncertainty takes over.

As mentioned, living organisms are far from both thermodynamic and quantum equilibrium. This means that quantum non-equilibrium particles, present in living organisms (e.g., in cells, tissues, organs…), could perform action-at-a-distance and non-local information exchanges thus creating the conditions of quantum coherence, non-local (superluminal) signaling and violation of the uncertainty principle.

These features can be considered as a main characteristic of life and, in turn of consciousness, distinguishing living matter (far from equilibrium) from the inanimate one. Following above reasoning, this paper is proposing a general model of consciousness as a quantum wave field, based on the extension of the de Broglie-Bohm theory for living matter (beyond the Born rule).

It is recalled that, in the de Broglie - Bohm theory, the quantum wave field associated to a particle is described by the wave function 𝞧, which follows the Schrodinger equation (1), and it orchestrates the motion of the particle:

$ih\frac{\partial \psi }{\partial t}=-\frac{h^2}{2m}{\nabla }^2\psi +V\psi \text{ (1)}$

expressing in above equation (1) the wave function 𝞧 of the quantum wave field in polar coordinates:

$\psi =R{e}^{\frac{iS}{h}}\text{ (2)}$

we obtain two differential equations. One of these is called the quantum Hamilton-Jacobi equation (3) [17], which describes the motion on a particle in a potential V and which is including a new term (the last one on the right) which is the quantum potential. The other differential equation (the continuity equation) is not of concern here.

$-\frac{\partial S}{\partial t}=\frac{{\left(\nabla S\right)}^2}{2m}+V-\frac{h^2}{2m}\frac{{\nabla }^{2}R}{R}\text{ (3)}$

$Q=-\frac{h^2}{2m}\frac{{\nabla }^{2}R}{R}\text{ (4)}$

Quantum potential Q (4) accounts for most of the differences between classical and quantum physics and it is a sort of potential energy function of the wave field which is available to quantum particles.

Quantum potential is considered as a special subset of consciousness potential or vice versa the consciousness potential is considered an extension of quantum potential. Therefore, the extension of these concepts for living organisms foresee the presence of a consciousness potential C which is active information “elaborated” and exchanged by the living organism through quantum symmetry breaking processes far from equilibrium. Consciousness potential C might be represented by an equation very similar to (4), where R, in this case, is the amplitude of the consciousness field (5). This is under study.

$C=-\frac{h^2}{2m}\frac{{\nabla }^{2}R}{R}\text{ (5)}$

It has been demonstrated that one of the main characteristics of living organisms is quantum coherence [4-8]. Therefore, in order to analyze the impact of potentials on coherent systems, this section provides a relevant example, even if limited to the electromagnetic vector potential.

The Aharonov Y, et al. [18] effect demonstrates that electromagnetic vector potential can be present even in spatial areas where the corresponding electromagnetic fields are absent. This means that, in principle, the electromagnetic vector potential has no energy content: it can be considered as a pure rhythm of oscillation that can travel at the phase velocity (not bound by the speed of light).

It is recalled that electromagnetic potentials have two components: the magnetic vector-potential A and electric potential Ao. As elaborated in [19] for a coherent system, where the phase φ assumes defined values, A and Ao become observable, through changes of the phase. On the other hand, a non-coherent system is affected by the electromagnetic fields, and not by the potentials, similar to the classical physics. In other words, the feature of coherence is allowing a systems to perceive the impact of electromagnetic potentials on its phase: this impact can be conveyed even in spatial areas where the corresponding electromagnetic fields are absent.

This is evident from the following Josephson equations:

$\nabla \phi =\alpha A\text{ (6)}$

$\frac{\partial \phi }{\partial t}=\beta A_0\text{ (7)}$

where a and b are constants.

This means that an electromagnetic vector potential, produced by fluctuating charged objects, can be detected only by coherent systems, as a sort of information. In [20] electromagnetic vector potential, in fact, is considered as a channel of informational effect on living objects. Electromagnetic vector-potential can change the phase of coherent systems, which becomes, thus, a register of the events occurring in the whole environment.

In summary, in the above analysis on classical and quantum potential we can notice that:

• Classical fields, like gravity or electromagnetism are generated by a source (e.g., masses or electric charges); on the other hand, the quantum field of the de Broglie Bohm theory seems not to be generated by any source;
• Electromagnetic fields can express an influence on a generic system with the intensity of a wave function, while the electromagnetic potentials can drive the evolution of the phase of a coherent system even where the electromagnetic fields are absent (Aharonov-Bohm effect);
• The effect of the quantum potential is independent of the intensity of the quantum field but depends only on the form of the wave function. This is different from classical waves, which transfer energy and momentum, and therefore produce effects that are proportional to the intensity of the wave.

Bohm and Hiley interpreted the quantum potential Q as active information capable of encoding the whole boundary conditions of a given experimental environment. Bohm and Hiley argued that active information (carried by the wave field and represented by Q) steers a quantum particle’s path and velocity by using the particle’s own energy.

This information becomes active as processed by the quantum entity: the working hypothesis was that the active information is transferred with little to no energy, but it can direct the move of an entity, which is using its own energy [17]. These considerations suggested them that any elementary particle (such as an electron) should have a complex inner structure to process this active information.

Following the same reasoning, in this paper it is argued that a living organism has an accompanying wave field (the consciousness wave field) and that together form a single physical system. In analogy which the quantum potential Q, also the consciousness potential C is active information capable of encoding the information about the whole environment.

This active information (carried by the wave field and represented by the C potential) steers the inner dynamics of the living system with its own energy. It becomes active as processed by the living system: obviously the inner structure of the living systems (processing C) should be much more complex than the one of the inanimate matter.

Moreover, the consciousness potential C is structured in a way to facilitate energy storage in the consciousness wave field and energy exchange with living organisms. This is obviously valid also for the quantum potential, which that limited part processes by inanimate quantum matter: for instance, in a many-particle quantum system this is evident as a non-local effect which is orchestrated by the quantum potential and does not necessarily decade with increasing distance. In fact, the quantum potential is not a classical potential in the sense that it doesn’t propagate, and it is not proportional to 1/r (where r is the distance).

In analogy with the consciousness wave field acts on the living organism and the living organism does not react back on it, at least in classical terms. As a matter of fact, as the quantum wave field and a particle are not separate entities, the same occurs for the consciousness wave field and a living organism: energy exchanges are related to changes in the shape of the wave field.

As from equation (4) Q and C are proportional to the curvature or form of the wave field. As well explained in [21], the form of the wave field may be described with reference to its wavefronts. A wavefront is defined as a surface over which the phase of the wave is constant: wavefronts depend on what’s happening (e.g., events) in the environment and what the wave field encounters.

If the active information of the consciousness potential C is related to the curvature or form of the Consciousness wave field, then it could be expressed in terms of Nambu-Goldstone bosons condensations, as described by the Quantum Field Theory (QFT). As a matter of fact, coherence (so important in living organisms) as emerging from SSB appears to be the origin of coded information. It’s information with a semantic level of meanings for the organisms, expressions of coherent dynamical processes.

This aspect concerning the modeling of the form of the quantum wave field by means of Nambu-Goldstone bosons will be elaborated in the next section.

QFT is recognized as a fundamental theory in quantum physics, standing at the basis of the Standard Model. QFT provides an information-theoretical re-interpretation of physical reality at the quantum level. Theory has been confirmed by several experimental validations [22].

According to QFT, the fundamental building blocks of Nature are not discrete particles at all. Instead, they are continuous fluid-like substances, spread throughout all of space, which are called fields. Examples of force fields are the gravitational, the electromagnetic, the strong and weak nuclear fields; examples of matter fields are the electron, neutrino, up quark and down quark. QFT describes particles as ripples of the quantum fields. For instance, a ripple of the electromagnetic field gets tied up into a bundle of energy that is what we call a photon; a ripple of the electron field gets tied up into an electron, and so on.

Even the vacuum is an active arena of ground state fluctuations of these quantum fields. In view of that, in QFT any quantum system is considered an “open” system, always interacting with other systems and the environment through these background fluctuations. This has remarkable consequences in the overall picture of Nature: for example, the fact that the Hamiltonian of any quantum system (even living organisms included) always comprises both the quantum system and the thermal bath of its surrounding environment [1,23].

Symmetry Breaking (SB) is a fundamental physical phenomenon well described by QFT [1]. SB concerns the transition of a quantum system from a certain symmetric state to another state at lower symmetry. In principles, lower symmetry means higher order and, therefore, lower entropy: therefore, SBs are creating some sort of ordering information that correlates the parts of a systems. There are two types of SBs: explicit SB and spontaneous SB. Explicit SB implies that a perturbation is determining a change of the basic dynamics of the system. In spontaneous SB, the dynamics are not changed by the perturbation itself, which is weak, acts only to trigger the SB. In this case, the strength or the intensity of the perturbation isn't important, rather it’s important its phase [2].

Nambu-Goldstone theorem proves that a SB implies the presence of Nambu-Goldstone bosons (ordering information): this has been validated by solid experimental evidence both in high-energy and condensed matter physics. Phonons in crystals, magnons in ferromagnets, etc., Experimentally, NG bosons can be observed with diffusion techniques (i.e., using them as targets of particles, for example neutrons), the energy spectrum is studied by exciting them, deforming the ordered structure (e.g., crystal lattice) by external tensions, thermal jumps, etc.

NG bosons are massless (in absence of edge effects) and collective vibrational modes coding ordering information [23,24]: the accumulation, or condensation of NG bosons in the vacuum state generates a state of minimum energy, called condensed state [5-8]. Such a condensed state is therefore stable, being a minimum energy state. NG bosons do not mediate force interactions, rather they represent ordered modalities of such interactions.

NG bosons should not be confused with the bosons Gauge fields. A Gauge boson is a bosonic elementary particle that acts as the force carrier: in the Gauge theory, elementary particles, interact with each other by the exchange of Gauge bosons, usually as virtual particles. Photons, W and Z bosons, and gluons are Gauge bosons.

It is recalled that the Gauge theory describes interactions and energy exchanges between quantum particles and their associated wave fields [25]. In the Gauge theory the Lagrangian (difference of the kinetic and the potential energy) of a system is kept invariant under continuous local symmetry transformations (called local Gauge transformation), thanks to the presence of the gauge fields. These fields are a sort of compensatory fields able to maintain said invariance.

In any SB phenomena there is a sort of balanced competition between the long-range ordering correlations of NG and Gauge bosons. The balance is reached depending on the boundary conditions and on the relative strengths of the Gauge and NG fields. The interplay between Gauge and massless NG bosons (as emerging from SB) in living matter plays a key role in coding and elaborating information responsible of biological features and functions [7].

For instance [26] provides an interesting dissipative quantum model of the brain, based on QFT. The model is an extension of the many-body brain model proposed in 1967 by Ricciardi, et al. [24]. The model leverages on the fact that in matter physics any particular information carried by certain ordered pattern is maintained by long range correlations mediated by massless NG bosons, generated through SB phenomena. In the brain dynamics, according to this model, the NG quanta are named the Dipole Wave Quanta (DWQ) as they are generated through the breakdown of the rotational symmetry of the electrical dipole vibrational field.

In general, the density of the condensation of NG bosons provides a measure of the degree of ordering of a field or system: the NG bosons condensation is described by a condensation function f(x) which acts as a “form factor” [27]. Therefore, in line with this prior art it is argued that the active information (or consciousness potential C), proposed in this paper, can be expressed in terms of NG bosons condensation functions (which are form factors of the consciousness wave field).

The paper started from the consideration that living organisms, from a thermodynamic perspective, are similar to open systems, operating far from equilibrium. In fact, life is based on exchanges of energy, matter, and information of organisms with the surrounding environment. Then, moving the analysis at a deeper physical level, these biological exchanges can be seen as mediated by wave-like quantum oscillations including, for example, mechanical, electromagnetic, nuclear and thermal ones. Even the vacuum, according to Quantum Field Theory (QFT), is the arena of quantum fluctuations of energy, whose minimum is named the ground state.

In view of that, in QFT any quantum system is considered an “open” system, always interacting with other systems and the environment through these background fluctuations. Therefore, it seems to be reasonable arguing that living organisms are open systems far not only from thermodynamic equilibriums but also from the quantum equilibrium. The paper proposes a model of the consciousness of living organisms, based on a broader approach than that of Quantum Mechanics and QFT: this new approach proposes to consider the quantum processes of consciousness, beyond quantum equilibrium, which is a fundamental characteristic of life and consciousness.

The proposed consciousness model leverages on the de Broglie-Bohm theory that led to the definition of the quantum field and quantum potential: in particular, consciousness is defined as a special quantum field, whose associated potential is processed by the living organisms, as active information.

The analysis concludes observing that the quantum field of consciousness (applicable to living matter) also has no sources and its shape, or curvature, has more importance, from a physical viewpoint, than its amplitude: in particular, it is proposed that this curvature is the active information of the field associated with condensations of the Nambu Goldstone bosons (as predicted by the QFT) following symmetry breaks phenomena.

Next steps of this research will mainly include: a deeper theoretical analysis and mathematical formulation of the consciousness model presented in this paper; experimental activities involving the detection of non-equilibrium particles in non-equilibrium systems.

1. Umezawa H, Yamanaka Y. Micro, macro and thermal concepts in quantum field theory. Advances in Physics. 1988;37(5):531-557. doi: 10.1080/00018738800101429.
2. Blasone M, Jizba P, Vitiello G. Quantum Field Theory and its Macroscopic Manifestations. London: Imperial College Press; 2011.
3. Lloyd S. Quantum coherence in biological systems. J Phys Conf Ser. 2011;302:012037. doi: 10.1088/1742-6596/302/1/012037.
4. Frohlich H. Long-range coherence and energy storage in biological systems. Int J Quantum Chem. 1968;2:641-649. doi: 10.1002/qua.560020505.
5. Del Giudice E, Doglia S, Milani M, Vitiello G. Spontaneous symmetry breakdown and boson condensation in biology. Physics Letters A. 1983;95A-9:508-510. doi: 10.1016/0375-9601(83)90509-1.
6. Del Giudice E, Doglia S, Milani M, Vitiello G. A quantum field theoretical approach to the collective behavior of biological systems. Nuclear Physics B. 1985;251(FS 13):375-400. doi: 10.1016/0550-3213(85)90267-6.
7. Del Giudice E, Doglia S, Milani M, Vitiello G. Electromagnetic field and spontaneous symmetry breakdown in biological matter. Nucl Phys B. 1986;275:185-199. doi: 10.1016/0550-3213(86)90595-X.
8. Del Giudice E, Preparata G, Vitiello G. Water as a free electric dipole laser. Phys Rev Lett. 1988 Aug 29;61(9):1085-1088. doi: 10.1103/PhysRevLett.61.1085. PMID: 10039515.
9. Ball P. Physics of life: The dawn of quantum biology. Nature. 2011 Jun 15;474(7351):272-4. doi: 10.1038/474272a. PMID: 21677723.
10. Salari V, Tuszynski J, Rahnama M, Bernroider G. Plausibility of quantum coherent states in biological systems. Journal of Physics: Conference Series. 2011;306. doi: 10.1088/1742-6596/306/1/012075.
11. Al-Khalili J. McFadden J. Life on the edge: The coming age of quantum biology. New York: Crown; 2015.
12. Valentini A. Beyond the quantum. Physics World. 2009;22(11):32. doi: 10.1088/2058-7058/22/11/36.
13. Hiley BJ, Pylkkanen P. Can mind affect matter via active information? Mind and Matter. 2005;3(2):8-27.
14. Eccles JC. Do mental events cause neural events analogously to the probability fields of quantum mechanics? Proc R Soc Lond B Biol Sci. 1986 May 22;227(1249):411-28. doi: 10.1098/rspb.1986.0031. PMID: 2873576.
15. Margenau H. The Miracle of Existence. New Science Library; 1984.
16. Antony V. Hidden Variables in Modern Cosmology. Youtube.com. Philosophy of Cosmology. 2013.
17. Bohm D, Hiley BJ. The undivided universe: An ontological interpretation of quantum theory. London and New York: Routledge; 1993.
18. Aharonov Y, Bohm D. Significance of electromagnetic potentials in the quantum theory. Physical Review. 1959;115(3):485. doi: 10.1103/PhysRev.115.485.
19. Brizhik L, Del Giudice E, Jørgensen SE, Marchettini N, Tiezzi E. The role of electromagnetic potentials in the evolutionary dynamics of ecosystems. Ecological Modelling. 2009;220(16): 1865-1869. doi: 10.1016/j.ecolmodel.2009.04.017.
20. Trukhan EM, Anosov VN. [Vector potential as a channel of informational effect on living objects]. Biofizika. 2007 Mar-Apr;52(2):376-81. Russian. PMID: 17477070.
21. Riggs PJ. Reflections on the de Broglie–Bohm Quantum Potential. Erkenntnis. 2008;68(1): 21-39. doi: 10.1007/s10670-007-9054-1.
22. Peskin ME. An introduction to quantum field theory. CRC Press; 2018.
23. Vitiello G. Dissipation and memory capacity in the quantum brain model. Int J Mod Phys. 1995;B9:973-989.
24. Ricciardi LM, Umezawa H. Brain physics and many-body problems. Kibernetik. 1967;4:44-48.
25. O'Raifeartaigh L, Straumann N. Gauge theory: Historical origins and some modern developments. Reviews of Modern Physics. 2000;72(1):1. doi: 10.1103/RevModPhys.72.1.
26. Freeman WJ, Vitiello G. The dissipative quantum model of brain and laboratory observations. In Physics of Emergence and Organization. 2008;233-251. doi: 10.1142/9789812779953_0009.
27. Freeman WJ, Vitiello G. Vortices in brain waves. International Journal of Modern Physics B. 2010;24(17):3269-3295. doi: 10.1142/S0217979210056025.